题目内容
在长为10cm的线段AB上任取一点P,以AP为半径作圆,使圆面积介于16cm2与49cm2之间的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:先算出事件发生的总区域的测度,即为线段AB的长度,再计算出圆的面积介于16πcm2到49πcm2的包含的区域长度,它们的比值就是圆的面积介于16πcm2到49πcm2的概率.
解答:
解:因为事件满足几何概型,事件发生的总区域为线段AB的长度10cm,
设“圆的面积介于16cm2到49cm2”为事件B,事件B包含的区域长度为
-
=3,
∴P(B)=
;
故选B.
设“圆的面积介于16cm2到49cm2”为事件B,事件B包含的区域长度为
| 49 |
| 16 |
∴P(B)=
| 3 |
| 10 |
故选B.
点评:本题主要考查了几何概型,几何概型的特点有下面两个:(1)试验中所有可能出现的基本事件有无限多个.(2)每个基本事件出现的可能性相等.关键是明确事件的集合是利用线段长度或者区域面积或者体积表示,属于基础题.

练习册系列答案
相关题目
在长方体ABCD-A1B1C1D1 中,B1C和C1D 与底面所成角分别为30°和45°,AA1=1,则A1到截面AB1D1的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数f(x)中,满足“对定义域内的任意一个x都有f(-x)+f(x)=0,且在区间(0,+∞)上恒有
f′(x)>0”的是( )
f′(x)>0”的是( )
A、f(x)=
| ||
| B、f(x)=x2 | ||
| C、f(x)=x3 | ||
| D、f(x)=ex |
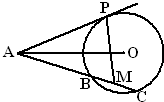 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,且与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点,
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,且与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点,