题目内容
正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为 ．
考点：球内接多面体,球的体积和表面积
专题：计算题,空间位置关系与距离
分析：正四棱锥P-ABCD的外接球的球心在它的高PE上，求出球的半径，求出球的表面积．
解答：
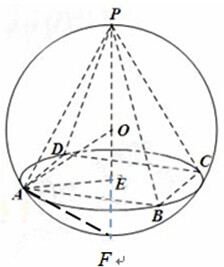解：如图，正四棱锥P-ABCD中，PE为正四棱锥的高，根据球的相关知识可知，正四棱锥的外接球的球心O必在正四棱锥的高线PE所在的直线上，延长PE交球面于一点F，连接AE，AF，由球的性质可知△PAF为直角三角形且AE⊥PF，根据平面几何中的射影定理可得PA2=PF•PE，因为AE=
=
=
，
所以侧棱长PA=
=
=
=3
，PF=2R，
所以18=2R×4，所以R=
，
所以S=4πR2=
故答案为：
解：如图，正四棱锥P-ABCD中，PE为正四棱锥的高，根据球的相关知识可知，正四棱锥的外接球的球心O必在正四棱锥的高线PE所在的直线上，延长PE交球面于一点F，连接AE，AF，由球的性质可知△PAF为直角三角形且AE⊥PF，根据平面几何中的射影定理可得PA2=PF•PE，因为AE=
| ||
| 2 |
| ||
| 2 |
| 2 |
所以侧棱长PA=
| PE2+AE2 |
| 42+2 |
| 18 |
| 2 |
所以18=2R×4，所以R=
| 9 |
| 4 |
所以S=4πR2=
| 81π |
| 4 |
故答案为：
| 81π |
| 4 |
点评：本题考查球的表面积，球的内接几何体问题，考查计算能力，是基础题．
练习册系列答案
相关题目
在长为10cm的线段AB上任取一点P，以AP为半径作圆，使圆面积介于16cm2与49cm2之间的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在2011年3月15日那天，南昌市物价部门对本市的5家商场的某商品的一天销售量及
由散点图可知，销售量y与价格x之间有较好的线性相关关系，根据上表可得回归直线方程是：
=-3.2x+a，则a=（ ）
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销量y | 11 | 10 | 8 | 6 | 5 |
 |
| y |
| A、-24 | B、35.6 |
| C、40.5 | D、40 |
设函数f（x）=
，若f（m）＞1，则m的取值范围是（ ）
|
| A、（-∞，-1） |
| B、（9，+∞） |
| C、（-∞，-1）∪（9，+∞） |
| D、（-∞，-1）∪（6，+∞） |
曲线y=
+
在点A（
，1）处的切线斜率为（ ）
| sinx |
| sinx+cosx |
| 1 |
| 2 |
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若a，b，c是互不相等的正数，且顺次成等差数列，x是a，b的等比中项，y是b，c的等比中项，则x2，b2，y2可以组成（ ）
| A、既是等差又是等比数列 |
| B、等比非等差数列 |
| C、等差非等比数列 |
| D、既非等差又非等比数列 |