题目内容
设M点的坐标为(x,y).
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中取随机取一个数作为y,求M点落在y轴的概率;
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组:
所表示的平面区域内的概率.
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中取随机取一个数作为y,求M点落在y轴的概率;
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组:
|
考点:几何概型
专题:概率与统计
分析:(1)总的基本事件共4×3=12种,所求事件包含3个,由古典概型公式可得;
(2)点M均匀地分布在x∈[0,3],y∈[0,4]所表示的平面区域内,而所求事件构成的平面区域是由不等式组
表示的平面区域,作图求面积可得.
(2)点M均匀地分布在x∈[0,3],y∈[0,4]所表示的平面区域内,而所求事件构成的平面区域是由不等式组
|
解答:
解:(1)记“M点落在y轴”为事件A.
M点的组成情况共4×3=12种,且每种情况出现的可能性相等,属于古典概型.
其中事件A包含的基本事件有(0,0),(0,1),(0,2)共3个.
∴P(A)=
=
.
(2)依条件可知,点M均匀地分布在x∈[0,3],y∈[0,4]所表示的平面区域内,属于几何概型.
该平面区域的图形为矩形围成的区域,其面积为S=3×4=12.
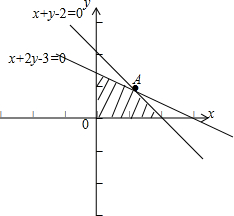
而所求事件构成的平面区域是由不等式组
表示的平面区域(如图阴影),
联立
,可解的A(1,1),∴S阴影=
×(1+
)×1+
×1×1=
,
∴所求事件的概率为p=
=
.
M点的组成情况共4×3=12种,且每种情况出现的可能性相等,属于古典概型.
其中事件A包含的基本事件有(0,0),(0,1),(0,2)共3个.
∴P(A)=
| 3 |
| 12 |
| 1 |
| 4 |
(2)依条件可知,点M均匀地分布在x∈[0,3],y∈[0,4]所表示的平面区域内,属于几何概型.
该平面区域的图形为矩形围成的区域,其面积为S=3×4=12.
而所求事件构成的平面区域是由不等式组
|
联立
|
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
∴所求事件的概率为p=
| S阴影 |
| S |
| 7 |
| 48 |

点评:本题考查古典概型和几何概型,涉及不等式组表示平面区域,作图是解决问题的关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某几何体的三视图如图,则这个几何体的体积是( )


A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
在长为10cm的线段AB上任取一点P,以AP为半径作圆,使圆面积介于16cm2与49cm2之间的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
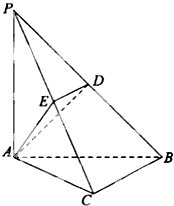 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.
