题目内容
1.已知函数$f(x)=x{e^x}-a(\frac{x^2}{2}+x)(a∈R)$.(Ⅰ)当a=1时,求函数f(x)的极值;
(Ⅱ)讨论函数f(x)的单调性.
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间和极值即可;
(Ⅱ)求出函数的导数,通过讨论a的范围求出函数的单调区间即可.
解答 解:(Ⅰ)当a=1时,$f(x)=x{e^x}-(\frac{x^2}{2}+x)$…1分
f'(x)=ex+xex-(x+1)=ex(x+1)-(x+1)=(x+1)(ex-1)…2分
令f'(x)=0得x=-1,或x=0.
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | ↘ | ↗ |
x=0时,f(x)有极小值f(0)=0…4分
(Ⅱ)f'(x)=ex+xex-a(x+1)=ex(x+1)-a(x+1)=(x+1)(ex-a)
(1)当a≤0时,ex-a>0,
由f'(x)>0得x>-1,即在(-1,+∞)上,函数f(x)单调递增,
由f'(x)<0得x<-1,即在(-∞,-1)上,函数f(x)单调递减;…6分
(2)当a>0时,令f'(x)=0得x=-1,或x=lna.
①当lna=-1即a=e-1时,无论x>-1或x<-1均有f'(x)>0,又f'(-1)=0
即在R上,f'(x)≥0,从而函数f(x)在R上单调递增;…8分
②当lna<-1即0<a<e-1时,
由f'(x)=(x+1)(ex-a)>0⇒x>-1或x<lna时,函数f(x)单调递增;
由f'(x)=(x+1)(ex-a)<0⇒lna<x<-1时,函数f(x)单调递减;…10分
③当lna>-1即a>e-1时,
由f'(x)=(x+1)(ex-a)>0⇒x>lna或x<-1时,函数f(x)单调递增;
由f'(x)=(x+1)(ex-a)<0⇒-1<x<lna时,函数f(x)单调递减;…12分
点评 考查导数的应用,考查分类讨论思想和运算能力,是一道难题.

练习册系列答案
相关题目
9.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A. | “m∥α,m∥β”是“α∥β”的充分不必要条件 | |
| B. | m∥n时,“m∥β”是“n∥β”的必要不充分条件 | |
| C. | n?α时,“m⊥α”是“m⊥n”的既不充分也不必要条件 | |
| D. | m⊥α,n⊥β时,“m⊥n”是“α⊥β”的充要条件 |
6.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x<2}\\{{x}^{2},x≥2}\end{array}\right.$,若f(a+1)≥f(2a-1),则实数a的取值范围是( )
| A. | (-∞,1] | B. | (-∞,2] | C. | [2,6] | D. | [2,+∞) |
11.已知平面向量$\overrightarrow{a}$=(k,3),$\overrightarrow{b}$=(1,4),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数k为( )
| A. | -12 | B. | 12 | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
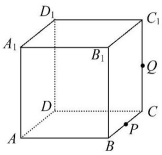 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②④(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②④(写出所有正确命题的编号).