题目内容
13.已知f(x)=$\sqrt{3}$sinx•cosx+cos2x,锐角△ABC的三个角A,B,C所对的边分别为a,b,c.(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)若f(C)=1,求m=$\frac{{a}^{2}+{b}^{2}+{c}^{2}}{ab}$的取值范围.
分析 (Ⅰ)将f(x)化简,结合三角函数的性质求解即可.
(Ⅱ)利用f(C)=1,求解角C,由余弦定理建立等式关系,利用三角函数的有界限求解范围.
解答 解:(Ⅰ)$f(x)=\sqrt{3}sinx•cosx+{cos^2}x=\frac{{\sqrt{3}}}{2}sin2x+\frac{1}{2}cos2x+\frac{1}{2}=sin(2x+\frac{π}{6})+\frac{1}{2}$.
∴函数f(x)的最小正周期$T=\frac{2π}{2}=π$.
由$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$是单调递增,
解得:$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6}$.
∴函数f(x)的单调递增区间$[{kπ-\frac{π}{3},kπ+\frac{π}{6}}],k∈Z$,最小正周期为π.
(Ⅱ)由(Ⅰ)可得f(C)=sin(2C+$\frac{π}{6}$)=1
∴$f(C)=sin(2C+\frac{π}{6})+\frac{1}{2}=1$.
∴$sin(2C+\frac{π}{6})=\frac{1}{2}$
∴$2C+\frac{π}{6}=2kπ+\frac{π}{6}$或$2C+\frac{π}{6}=2kπ+\frac{5π}{6}$k∈Z,
∵△ABC是锐角三角形,
∴$C=\frac{π}{3}$.
由余弦定理c2=a2+b2-2abcosC,可得c2=a2+b2-ab
∴$m=\frac{{{a^2}+{b^2}+{c^2}}}{ab}=\frac{{2({a^2}+{b^2})}}{ab}-1=2(\frac{b}{a}+\frac{a}{b})-1$…①.
∵△ABC为锐角三角形
∴$\left\{\begin{array}{l}0<A<\frac{π}{2}\\ 0<\frac{2π}{3}-A<\frac{π}{2}\end{array}\right.$∴$\frac{π}{6}<A<\frac{π}{2}$.
由正弦定理得:$\frac{b}{a}=\frac{sinB}{sinA}=\frac{{sin(\frac{2}{3}π-A)}}{sinA}=\frac{{\sqrt{3}}}{2tanA}+\frac{1}{2}∈({\frac{1}{2},2})$…②.
由②式设t=$\frac{b}{a}$,则$t∈(\frac{1}{2},2)$,
那么①式化简为m=$2(t+\frac{1}{t})-1$.
由y=$t+\frac{1}{t}≥2,(t=1)$时取等号.
∴m≥3.
根据勾勾函数的性质可得:($\frac{1}{2}$,1)是单调递减,(1,2)是单调递增,
∴m<4
故得$m=\frac{{{a^2}+{b^2}+{c^2}}}{ab}∈[{3,4})$.
点评 本题主要考查三角函数的图象和性质,正余弦定理的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{1}{9}$ | B. | $\frac{5}{36}$ | C. | $\frac{3}{18}$ | D. | $\frac{1}{72}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
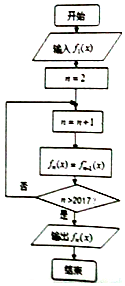 执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )
执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}$) |
| A. | 先向左平移$\frac{π}{6}$个单位,再将各点横坐标变为原来的$\frac{1}{2}$倍 | |
| B. | 先向右平移$\frac{π}{6}$个单位,再将各点横坐标变为原来的2倍 | |
| C. | 先向左平移$\frac{π}{3}$个单位,再将各点横坐标变为原来的$\frac{1}{2}$倍 | |
| D. | 先向右平移$\frac{π}{3}$个单位,再将各点横坐标变为原来的2倍 |
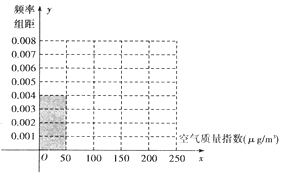 全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | y | 10 | 5 |
(Ⅱ)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.