题目内容
10.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,在x轴上有一点M(-3,0)满足$\overrightarrow{M{F_2}}=2\overrightarrow{M{F_1}}$.(1)求椭圆C的方程;
(2)直线l与直线x=2交于点A,与直线x=-2交于点B,且$\overrightarrow{{F_2}A}•\overrightarrow{{F_2}B}=0$,判断并证明直线l与椭圆C的交点个数.
分析 (1)设椭圆的焦距为2c,由题意列a,c的方程组,求得a,c的值,再由隐含条件求得b,则椭圆方程可求;
(2)设出直线l的方程为:y=kx+m,可得A(2,2k+m),B(-2,m-2k),由$\overrightarrow{{F_2}A}•\overrightarrow{{F_2}B}=0$,得(1,2k+m)•(-3,m-2k)=0,即m2=4k2+3.联立直线方程与椭圆方程,化为关于x的一元二次方程,利用判别式等于0得答案.
解答 解:(1)设椭圆的焦距为2c,由题意有:$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{1}{2}}\\{c+3=2(-c+3)}\end{array}\right.$,解得a=2,c=1.
∴b2=a2-c2=3.
则椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由题意可知直线l的斜率存在,设直线l的方程为:y=kx+m.
则A(2,2k+m),B(-2,m-2k),
由$\overrightarrow{{F_2}A}•\overrightarrow{{F_2}B}=0$,得(1,2k+m)•(-3,m-2k)=0,
即m2=4k2+3.
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0.
∵△=64k2m2-4(3+4k2)(4m2-12)=4(48k2-12m2+36)=0.
∴直线l与椭圆C的交点个数是1.
点评 本题考查椭圆的简单性质,可直线与椭圆位置关系的应用,训练了向量垂直与数量积间关系的应用,是中档题.

| A. | 先向左平移$\frac{π}{6}$个单位,再将各点横坐标变为原来的$\frac{1}{2}$倍 | |
| B. | 先向右平移$\frac{π}{6}$个单位,再将各点横坐标变为原来的2倍 | |
| C. | 先向左平移$\frac{π}{3}$个单位,再将各点横坐标变为原来的$\frac{1}{2}$倍 | |
| D. | 先向右平移$\frac{π}{3}$个单位,再将各点横坐标变为原来的2倍 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
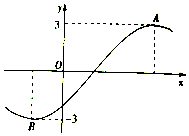 已知函数f(x)=3sin(ωx+ϕ)$(ω>0,|ϕ|≤\frac{π}{2})$的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )
已知函数f(x)=3sin(ωx+ϕ)$(ω>0,|ϕ|≤\frac{π}{2})$的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )