题目内容
9.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )| A. | “m∥α,m∥β”是“α∥β”的充分不必要条件 | |
| B. | m∥n时,“m∥β”是“n∥β”的必要不充分条件 | |
| C. | n?α时,“m⊥α”是“m⊥n”的既不充分也不必要条件 | |
| D. | m⊥α,n⊥β时,“m⊥n”是“α⊥β”的充要条件 |
分析 利用线面面面平行与垂直的判定及其性质定理即可判断出关系.
解答 解:A.“m∥α,m∥β”是“α∥β”的既不充分也不必要条件,因此不正确;
B.m∥n时,“m∥β”是“n∥β”的既不充分也不必要条件,因此不正确;
C.n?α时,“m⊥α”是“m⊥n”的充分但不必要条件,因此不正确;
D.m⊥α,n⊥β时,“m⊥n”是“α⊥β”的充要条件,正确.
故选:D.
点评 本题考查了线面面面平行与垂直的判定及其性质定理、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.复数$z=2i+\frac{2}{1+i}$(i是虚数单位)在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.要得到函数$y=sin({2x+\frac{π}{3}})$的图象,只要将函数y=sinx的图象( )
| A. | 先向左平移$\frac{π}{6}$个单位,再将各点横坐标变为原来的$\frac{1}{2}$倍 | |
| B. | 先向右平移$\frac{π}{6}$个单位,再将各点横坐标变为原来的2倍 | |
| C. | 先向左平移$\frac{π}{3}$个单位,再将各点横坐标变为原来的$\frac{1}{2}$倍 | |
| D. | 先向右平移$\frac{π}{3}$个单位,再将各点横坐标变为原来的2倍 |
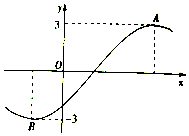 已知函数f(x)=3sin(ωx+ϕ)$(ω>0,|ϕ|≤\frac{π}{2})$的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )
已知函数f(x)=3sin(ωx+ϕ)$(ω>0,|ϕ|≤\frac{π}{2})$的部分图象如图所示,A,B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)的单位长度后所得函数图象关于y轴对称,则t的最小值为( )