题目内容
16.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的焦点为F1,F2,若椭圆上存在满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=\frac{1}{2}{b^2}$的点P,则椭圆的离心率的范围是$[\frac{{\sqrt{3}}}{3},1)$.分析 由F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个焦点,椭圆上存在点P,满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=\frac{1}{2}{b^2}$,推出a,c的关系,由此能求出离心率的范围.
解答 解:∵椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的焦点为F1,F2,若椭圆上存在满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=\frac{1}{2}{b^2}$的点P,
∴|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|cos$<\overrightarrow{P{F}_{1}},\overrightarrow{P{F}_{2}}>$=$\frac{1}{2}$b2,4c2=${\overrightarrow{P{F}_{1}}}^{2}$$+{\overrightarrow{P{F}_{2}}}^{2}$-2|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|cos$<\overrightarrow{P{F}_{1}},\overrightarrow{P{F}_{2}}>$,$|\overrightarrow{P{F}_{1}}|+|\overrightarrow{P{F}_{2}}|=2a$
可得${\overrightarrow{P{F}_{1}}}^{2}$$+{\overrightarrow{P{F}_{2}}}^{2}$+2|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=4a2,∴4c2=4a2-2|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|-b2,
∴2|PF1|•|PF2|=3a2-3c2≤2$(\frac{|\overrightarrow{P{F}_{1}}|+|\overrightarrow{P{F}_{2}}|}{2})^{2}$,可得$\frac{{c}^{2}}{{a}^{2}}≥\frac{1}{3}$,解得e$≥\frac{\sqrt{3}}{3}$.
所以e∈$[\frac{{\sqrt{3}}}{3},1)$.
故答案为:$[\frac{{\sqrt{3}}}{3},1)$.
点评 本题考查椭圆的性质的简单应用,解题时要认真审题,注意等价转化思想的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 4 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | (1,+∞) | B. | (-∞,1) | C. | (e,+∞) | D. | (-∞,e) |
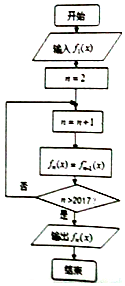 执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )
执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}$) |
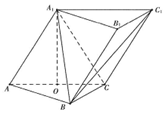 在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.
在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.