题目内容
农业技术员进行某种作物的种植密度试验,把一块试验田划分为8块面积相等的区域(除了种植密度,其它影响作物生长的因素都保持一致),种植密度和单株产量统计如下:
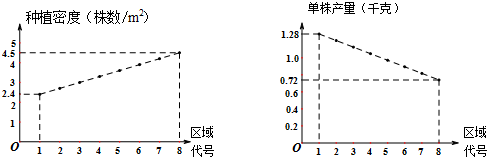
根据上表所提供信息,第 号区域的总产量最大,该区域种植密度为 株/m2.

根据上表所提供信息,第
考点:根据实际问题选择函数类型,收集数据的方法
专题:函数的性质及应用
分析:根据图象求出种植密度函数以及单株产量函数即可得到结论.
解答:
解:种植密度函数对应的直线经过点(1,2.4),(8,4.5),
则对应直线的斜率k=
=
=0.3,
则直线方程为y-2.4=0.3(x-1),即y=0.3x+2.1,
单株产量函数对应的直线经过点(1,1.28),(8,0.72),
则对应直线的斜率k=
=
=-0.08,
则直线方程为y-1.28=-0.08(x-1),即y=-0.08x+1.36,
即总产量m(x)=(0.3x+2.1)(-0.08x+1.36)=-0.024(x+7)(x-17)=-0.024(x2-10x-119),
∴当x=5时,函数m(x)有最大值,即5号区域的总产量最大,
此时当x=5代入y=0.3x+2.1得y=0.3×5+2.1=3.6,
故答案为:5,3.6.
则对应直线的斜率k=
| 4.5-2.4 |
| 8-1 |
| 2.1 |
| 7 |
则直线方程为y-2.4=0.3(x-1),即y=0.3x+2.1,
单株产量函数对应的直线经过点(1,1.28),(8,0.72),
则对应直线的斜率k=
| 1.28-0.72 |
| 1-8 |
| 0.56 |
| -7 |
则直线方程为y-1.28=-0.08(x-1),即y=-0.08x+1.36,
即总产量m(x)=(0.3x+2.1)(-0.08x+1.36)=-0.024(x+7)(x-17)=-0.024(x2-10x-119),
∴当x=5时,函数m(x)有最大值,即5号区域的总产量最大,
此时当x=5代入y=0.3x+2.1得y=0.3×5+2.1=3.6,
故答案为:5,3.6.
点评:本题主要考查函数的应用,利用条件求出对应的直线方程,利用二次函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
如图所示是某一几何体的三视图,则它的体积为( )
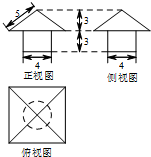

| A、16+12π |
| B、48+12π |
| C、64+12π |
| D、64+16π |
 如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.