题目内容
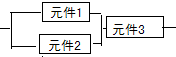 某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,σ2),若每个元件使用寿命超过1200小时的概率为
某一部件由三个电子元件按如图所示方式连接而成,元件1或元件2正常工作,则部件正常工作:设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,σ2),若每个元件使用寿命超过1200小时的概率为| 1 |
| 3 |
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:由题意可得每个元件寿命不足800小时的概率为
,故元件1,2,3的使用寿命超过800小时的概率均为1-
,可得所求事件的概率为(1-
×
)×
,计算求得结果
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
解答:
解:设该部件的使用寿命超过800小时的概率为P(A).因为三个元件的使用寿命均服从正态分布N(1000,σ2),
每个元件使用寿命超过1200小时的概率为
,故每个元件寿命不足800小时的概率为
,
所以,元件1,2,3的使用寿命超过800小时的概率均为1-
=
,
∴P(A)=(1-
×
)×
=
,
故答案为:
.
每个元件使用寿命超过1200小时的概率为
| 1 |
| 3 |
| 1 |
| 3 |
所以,元件1,2,3的使用寿命超过800小时的概率均为1-
| 1 |
| 3 |
| 2 |
| 3 |
∴P(A)=(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 27 |
故答案为:
| 16 |
| 27 |
点评:本题主要考查相互独立事件的概率乘法公式的应用,等可能事件的概率,所求的事件的概率等于用1减去它的对立事件概率,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则下列结论中正确的是( )
| sin(x+π) |
| cos(π-x) |
| A、f(x)的最小正周期是2π | ||
| B、f(x)在[4,5]上单调递增 | ||
C、f(x)的图象关于x=
| ||
D、f(x)的图象关于点(
|
设全集U={3,4,5,6},集合A={3,5,6},B={4,5,6},则∁UA∩B=( )
| A、{4,7} | B、{3,6} |
| C、{4} | D、{7} |
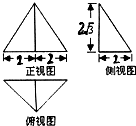 一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为
一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为