题目内容
设n=
6sinxdx,则二项式(x-
)n的展开式中,x2项的系数为( )
| ∫ |
0 |
| 2 |
| x |
| A、60 | B、75 | C、90 | D、120 |
考点:定积分,二项式系数的性质
专题:计算题,二项式定理
分析:由定积分求出n的值,代入(x-
)n,求出二项展开式的通项,由x得系数确定r值,则x2项的系数可求.
| 2 |
| x |
解答:
解:∵n=
6sinxdx=-6cosx
=-6cos
+6cos0=6.
∴(x-
)n=(x-
)6.
通项Tr+1=
x6-r(-
)r=(-2)r
x6-2r.
令6-2r=2,得r=2.
∴x2项的系数为(-2)2×
=60.
故选:A.
| ∫ |
0 |
| | |
0 |
| π |
| 2 |
∴(x-
| 2 |
| x |
| 2 |
| x |
通项Tr+1=
| C | r 6 |
| 2 |
| x |
| C | r 6 |
令6-2r=2,得r=2.
∴x2项的系数为(-2)2×
| C | 2 6 |
故选:A.
点评:本题考查了定积分,考查了二项式系数的性质,是基础题.

练习册系列答案
相关题目
等比数列{an}满足a2+a4=20,a3+a5=40,则公比q=( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
设z1=i5+i6…+i12,z2=i5•i6…i12,则z1,z2的关系是( )
| A、z1=z2 |
| B、z1=-z2 |
| C、z1=z2-1 |
| D、无法确定 |
3位数学家,4位物理学家,站成两排照像.其中前排3人后排4人,要求数学家要相邻,则不同的排队方法共有( )
| A、5040种 | B、840种 |
| C、720种 | D、432种 |
已知数列
,
,
,
,…,那么0.98,0.96,0.94中属于该数列中某一项值的应当有( )
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| A、0个 | B、1个 | C、2个 | D、3个 |
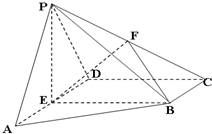 已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.
已知在四棱锥P-ABCD中,AD∥BC,AD⊥CD,PA=PD=AD=2BC=2CD,E,F分别是AD,PC的中点.