题目内容
已知函数f(x)=cos2x+sinx-1,(x∈R).
(Ⅰ)求f(
)的值;
(Ⅱ)当x∈[-
,
]时,求f(x)的取值范围.
(Ⅰ)求f(
| 7π |
| 6 |
(Ⅱ)当x∈[-
| π |
| 6 |
| 2π |
| 3 |
考点:同角三角函数基本关系的运用,三角函数的最值
专题:三角函数的求值
分析:(Ⅰ)f(x)解析式利用同角三角函数间的基本关系化简,整理为二次函数的顶点形式,将x=
代入计算即可求出f(
)的值;
(Ⅱ)由x的范围求出sinx的范围,进而确定出f(x)的范围.
| 7π |
| 6 |
| 7π |
| 6 |
(Ⅱ)由x的范围求出sinx的范围,进而确定出f(x)的范围.
解答:
解:(Ⅰ)∵f(x)=cos2x+sinx-1=1-sin2x+sinx-1=-sin2x+sinx=-(sinx-
)2+
,
∴f(
)=-(-
-
)2+
=-
;
(Ⅱ)∵x∈[-
,
],∴sinx∈[-
,1],
∴sinx-
∈[-1,
],
∴(sinx-
)2∈[0,1],
∴-(sinx-
)2∈[-1,0],
即-(sinx-
)2+
∈[-
,
],
则f(x)的取值范围为[-
,
].
| 1 |
| 2 |
| 1 |
| 4 |
∴f(
| 7π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
(Ⅱ)∵x∈[-
| π |
| 6 |
| 2π |
| 3 |
| 1 |
| 2 |
∴sinx-
| 1 |
| 2 |
| 1 |
| 2 |
∴(sinx-
| 1 |
| 2 |
∴-(sinx-
| 1 |
| 2 |
即-(sinx-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
则f(x)的取值范围为[-
| 3 |
| 4 |
| 1 |
| 4 |
点评:此题考查了同角三角函数基本关系的运用,以及正弦函数的值域,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
设n=
6sinxdx,则二项式(x-
)n的展开式中,x2项的系数为( )
| ∫ |
0 |
| 2 |
| x |
| A、60 | B、75 | C、90 | D、120 |
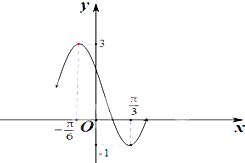 已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<