题目内容
3位数学家,4位物理学家,站成两排照像.其中前排3人后排4人,要求数学家要相邻,则不同的排队方法共有( )
| A、5040种 | B、840种 |
| C、720种 | D、432种 |
考点:计数原理的应用
专题:排列组合
分析:根据分类和分步计数原理,利用捆绑法,把3位数学家捆绑在一起看作一个元素,以数学家排在前排和后排各一类,进行排列,问题得以解决.
解答:
解:利用捆绑法,把3位数学家捆绑在一起看作一个元素,有
,当数学家在前排时,有
=144种,当数学家在后一排时,先从4位物理学家中选3位排在前排,剩下的一位再和数学家全排,有
•
=288种,共有144+288=432种.
故选D.
| A | 3 3 |
| A | 3 3 |
| •A | 4 4 |
| A | 3 4 |
| •A | 3 3 |
| A | 2 2 |
故选D.
点评:本题考查了分类分类与分步计数原理,关键是正确区分分步和分类,属于基础题.

练习册系列答案
相关题目
为得到函数y=cos(2x+
)的图象,只需将函数y=sin2x的图象( )
| 2π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知y=f(x)是定义在R上的偶函数,且在[0,+∞)上单调递增,则满足f(m)<f(1)的实数m的范围是( )
| A、-1<m<0 |
| B、0<m<1 |
| C、-1<m<1 |
| D、-1≤m≤1 |
“a=2”是“直线2x+ay-1=0与直线ax+3y-2=0平行”的( )
| A、充分必要条件 |
| B、充分而不必要条件 |
| C、必要而不充分条件 |
| D、既不充分也不必要条件 |
设i是虚数单位,那么复数(1-i)i等于( )
| A、-1+i | B、1+i |
| C、-1-i | D、1-i |
在等比数列{an}中,若a1=
,a4=-4,则|a1|+|a2|+…+|an|=( )
| 1 |
| 2 |
A、2n-1-
| ||
B、2n-
| ||
C、4n-1-
| ||
D、4n-
|
设n=
6sinxdx,则二项式(x-
)n的展开式中,x2项的系数为( )
| ∫ |
0 |
| 2 |
| x |
| A、60 | B、75 | C、90 | D、120 |
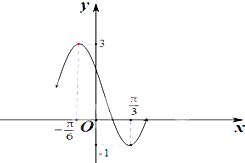 已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<