题目内容
已知f(x)+2f(
)=2x-1对于任意x∈R且x≠0都成立,求函数f(x)的解析式.
| 1 |
| x |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:首先,在所给的等式中,等号两边同时以
代x,得到一个等式f(
)+2f(x)=
-1,然后,联立方程组,把f(x)当做未知数,求解即可.
| 1 |
| x |
| 1 |
| x |
| 2 |
| x |
解答:
解:∵f(x)+2f(
)=2x-1,①
等号两边同时以
代x,
得:f(
)+2f(x)=
-1,②
联立①②,
由①-2×②,解得
f(x)=
x-
+
,
∴函数f(x)的解析式:
f(x)=
x-
+
(x≠0).
| 1 |
| x |
等号两边同时以
| 1 |
| x |
得:f(
| 1 |
| x |
| 2 |
| x |
联立①②,
由①-2×②,解得
f(x)=
| 2 |
| 3 |
| 4 |
| 3x |
| 1 |
| 3 |
∴函数f(x)的解析式:
f(x)=
| 2 |
| 3 |
| 4 |
| 3x |
| 1 |
| 3 |
点评:本题重点考查函数解析式的求解方法,构造法在解题中的应用,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知y=f(x)是定义在R上的偶函数,且在[0,+∞)上单调递增,则满足f(m)<f(1)的实数m的范围是( )
| A、-1<m<0 |
| B、0<m<1 |
| C、-1<m<1 |
| D、-1≤m≤1 |
设n=
6sinxdx,则二项式(x-
)n的展开式中,x2项的系数为( )
| ∫ |
0 |
| 2 |
| x |
| A、60 | B、75 | C、90 | D、120 |
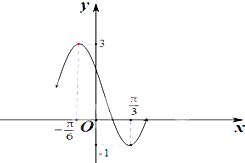 已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<