题目内容
在某学校组织的一次篮球定点投篮训练中,规定每人最多投3次,在A处每投进一球得3分,在B处每投进一球得2分,如果前两次得分之和超过3分即停止投篮,否则投三次,某同学在A处的命中率为p,在B处的命中率为q,该同学选择先在A处投一球,以后都在B处投,用X表示该同学投篮训练结束后所得的总分,其分布列为:
(1)若p=0.25,P1=0.03,求该同学用上述方式投篮得分是5分的概率
(2)若该同学在B处连续投篮3次,投中一次得2分,用Y表示该同学投篮结束后所得的总分,试比较E(X)与E(Y)的大小.
| X | 0 | 2 | 3 | 4 | 5 |
| P | P1 | P2 | P3 | P4 | P5 |
(2)若该同学在B处连续投篮3次,投中一次得2分,用Y表示该同学投篮结束后所得的总分,试比较E(X)与E(Y)的大小.
考点:离散型随机变量的期望与方差,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由题设知,“X=0”对应的事件为“在三次投篮中没有一次投中”,由对立事件和相互独立事件性质,
知P(X=0)=(1-p)(1-q)2=0.03,由p=0.25,解得q=0.8.由此能求出该同学用上述方式投篮得分是5分的概率.
(2)根据题意利用相互独立事件乘法公式分别求出p1,p2,p3,p4,p5,由此求出E(X);由已知得Y的可能取值为0,2,4,分别求出P(Y=0),P(Y=2),P(Y=4),由此求出E(Y),从而能比较E(X)与E(Y)的大小.
知P(X=0)=(1-p)(1-q)2=0.03,由p=0.25,解得q=0.8.由此能求出该同学用上述方式投篮得分是5分的概率.
(2)根据题意利用相互独立事件乘法公式分别求出p1,p2,p3,p4,p5,由此求出E(X);由已知得Y的可能取值为0,2,4,分别求出P(Y=0),P(Y=2),P(Y=4),由此求出E(Y),从而能比较E(X)与E(Y)的大小.
解答:
解:(1)由题设知,“X=0”对应的事件为“在三次投篮中没有一次投中”,
由对立事件和相互独立事件性质,
知P(X=0)=(1-p)(1-q)2=0.03,
由p=0.25,解得q=0.8.
∴该同学用上述方式投篮得分是5分的概率
P(X=5)=pq+p(1-q)q=0.25×0.8+0.25×0.2×0.8=0.24.
(2)根据题意p1=P(X=0)=(1-p)(1-q)2=(1-0.75)(1-0.8)2=0.03,
p2=P(X=2)=(1-p)•
(1-q)q=2(1-p)(1-q)q=2(1-0.25)(1-0.8)×0.8=0.24,
p3=p(X=3)=p(1-q)2=0.25×(1-0.8)2=0.01
p4=p(X=4)=(1-p)q2=0.75×0.82=0.48,
p5=p(X=5)=pq+q(1-q)q=0.25×0.8+0.25×0.2×0.8=0.24,
因此E(X)=0×0.03+2×0.24+3×0.01+4×0.48+5×0.24=3.63.
由已知得Y的可能取值为0,2,4,
P(Y=0)=(1-0.8)3=0.008,
P(Y=2)=
(0.8)(1-0.8)2=0.096,
P(Y=4)=0.82+0.2×0.8×0.8+0.8×0.2×0.8=0.896,
∴E(Y)=0×0.008+2×0.096+4×0.896=3.776.
∴E(X)<E(Y).
由对立事件和相互独立事件性质,
知P(X=0)=(1-p)(1-q)2=0.03,
由p=0.25,解得q=0.8.
∴该同学用上述方式投篮得分是5分的概率
P(X=5)=pq+p(1-q)q=0.25×0.8+0.25×0.2×0.8=0.24.
(2)根据题意p1=P(X=0)=(1-p)(1-q)2=(1-0.75)(1-0.8)2=0.03,
p2=P(X=2)=(1-p)•
| C | 1 2 |
p3=p(X=3)=p(1-q)2=0.25×(1-0.8)2=0.01
p4=p(X=4)=(1-p)q2=0.75×0.82=0.48,
p5=p(X=5)=pq+q(1-q)q=0.25×0.8+0.25×0.2×0.8=0.24,
因此E(X)=0×0.03+2×0.24+3×0.01+4×0.48+5×0.24=3.63.
由已知得Y的可能取值为0,2,4,
P(Y=0)=(1-0.8)3=0.008,
P(Y=2)=
| C | 1 3 |
P(Y=4)=0.82+0.2×0.8×0.8+0.8×0.2×0.8=0.896,
∴E(Y)=0×0.008+2×0.096+4×0.896=3.776.
∴E(X)<E(Y).
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法及应用,是中档题,解题时要认真审题,注意可能事件概率计算公式和相互独立事件概率乘法公式的合理运用.

练习册系列答案
相关题目
函数y=
+
的定义域为( )
| 1-x |
| x |
| A、{x|x≤1} |
| B、{x|x≥0} |
| C、{x|x≥1或x≤0} |
| D、{x|0≤x≤1} |
设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)•f(y)=f(x+y),若a1=
,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
| 1 |
| 2 |
A、[
| ||
B、[
| ||
C、[
| ||
D、[
|
若执行如图所示的程序框图,输出S的值为( )


| A、2log23 |
| B、log27 |
| C、3 |
| D、2 |
若y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的最小值巍峨-2,其图象相邻最高点与最低点横坐标之差为2π,且图象过点(0,1),则其解析式是( )
| π |
| 2 |
A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(x+
| ||||
D、y=2sin(x+
|
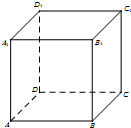 已知正方体ABCD-A1B1C1D1的棱长为1.给出下列五个命题:
已知正方体ABCD-A1B1C1D1的棱长为1.给出下列五个命题: