题目内容
设数列{an}的前n项和为Sn,且Sn=n-an(n∈N+).
(1)求证:数列{an-1}为等比数列,并写出{an}的通项公式;
(2)设bn=a(an-1)-(2n+1)(a为常数).若b3>0,当且仅当a=3时,|bn|取到最小值,求a的取值范围.
(1)求证:数列{an-1}为等比数列,并写出{an}的通项公式;
(2)设bn=a(an-1)-(2n+1)(a为常数).若b3>0,当且仅当a=3时,|bn|取到最小值,求a的取值范围.
考点:数列递推式,等比关系的确定
专题:计算题,点列、递归数列与数学归纳法
分析:(1)由Sn=n-an(n∈N+).得Sn-1=n-1-an-1(n≥2).两式相减,得2an=a n-1+1,变形得出an-1=
(an-1-1),从而数列{an-1}为等比数列,通过求出数列{an-1}的通项公式求出{an}的通项公式.
(2)bn=a(an-1)-(2n+1)=-
-(2n+1),由b3>0得出a<-56,数列{bn}为递减数列,由已知仅当a=3时,|bn|取到最小值,所以b4<0,b3<|b4|=-b4,即b3+b4<0
通过不等式组求出a的范围.
| 1 |
| 2 |
(2)bn=a(an-1)-(2n+1)=-
| a |
| 2n |
通过不等式组求出a的范围.
解答:
解:(1)因为Sn=n-an(n∈N+).Sn-1=n-1-an-1(n≥2).
两式相减,得2an=a n-1+1,即an-1=
(an-1-1),
又a1=1-a1,所以a1=
,a1-1=-
,
所以数列{an-1}是以-
为首项,以
为公比的等比数列,
所以an-1=-
•(
)n-1,得出{an}的通项公式an=1-
,
(2)bn=a(an-1)-(2n+1)=-
-(2n+1)
由b3>0,得a<-56(<0)①,∴数列{bn}为递减数列.
因为当且仅当a=3时,|bn|取到最小值,所以b4<0②,b3<|b4|=-b4,即b3+b4<0③
①②③联立解得-
<a<-56.
两式相减,得2an=a n-1+1,即an-1=
| 1 |
| 2 |
又a1=1-a1,所以a1=
| 1 |
| 2 |
| 1 |
| 2 |
所以数列{an-1}是以-
| 1 |
| 2 |
| 1 |
| 2 |
所以an-1=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
(2)bn=a(an-1)-(2n+1)=-
| a |
| 2n |
由b3>0,得a<-56(<0)①,∴数列{bn}为递减数列.
因为当且仅当a=3时,|bn|取到最小值,所以b4<0②,b3<|b4|=-b4,即b3+b4<0③
①②③联立解得-
| 256 |
| 3 |
点评:本题考查数列通项公式求解,数列的单调性及应用,考查转化构造,推理计算能力.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
设f(x)是定义在R上的恒不为零的函数,对任意实数x,y∈R,都有f(x)•f(y)=f(x+y),若a1=
,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
| 1 |
| 2 |
A、[
| ||
B、[
| ||
C、[
| ||
D、[
|
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
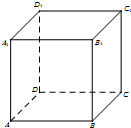 已知正方体ABCD-A1B1C1D1的棱长为1.给出下列五个命题:
已知正方体ABCD-A1B1C1D1的棱长为1.给出下列五个命题: