题目内容

若（a+i）（2+i）是纯虚数（i是虚数单位），则实数a的值为
 
．
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由已知（a-i）（1+i）是纯虚数，将（a-i）（1+i）展开，则其实部应该为0，而虚部一定不为0，由此构造关于a的方程，解方程即可得到答案．
解答： 解：∵（a+i）（2+i）
=（2a-1）+（a+2）i
若（a+i）（2+i）是纯虚数
则2a-1=0，a+2≠0
解得a=
1
2
；
故答案为：
1
2
．
点评：本题考查的知识点是复数的基本概念，其中根据复数Z=a+bi为纯虚数，则实数a为0，虚部b一定不为0，得到关于参数的方程是解答本题的关键．
练习册系列答案
相关题目
某四棱锥的三视图如图所示（单位：cm），则该四棱锥的体积是（　　）
A、27cm3
B、9cm3
C、3
2
cm3
D、3cm3
在一条笔直的工艺流水线上有n个工作台，将工艺流水线用如图所示的数轴表示，各工作台的坐标分别为x1，x2，…，xn，每个工作台上有若干名工人．现要在流水线上建一个零件供应站，使得各工作台上的所有工人到供应站的距离之和最短．

（Ⅰ）若n=2，每个工作台上只有一名工人，试确定供应站的位置；
（Ⅱ）若n=5，工作台从左到右的人数依次为3，2，1，2，2，试确定供应站的位置，并求所有工人到供应站的距离之和的最小值．
椭圆
x2
4
+
y2
b2
=1（b＞0）的焦点在x轴上，左焦点为（-c，0），其右顶点关于直线x-y+4=0的对称点在直线x=-
4
c
上，
（1）求椭圆的方程；
（2）过椭圆的左焦点F的直线l交椭圆于A、B两点，交直线x=-
4
c
于点C，设O为坐标原点，且
OA
+
OC
=2
OB
，求△OAB的面积．
在边长为2的正方形ABCD内随机取一点M，则AM＜1的概率为
 
．
在区间[-3，3]上随机取一个数x，使得|x-1|+|x+2|≤5成立的概率为
 
．
如图是正方体的平面展开图，在这个正方体中，以下四个命题：
（1）BM与ED平行；
（2）CN与BE是异面直线；
（3）CN与BM成60°；
（4）CN与AF垂直．
其中正确的有
 
．
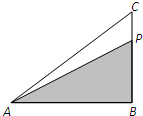如图，在Rt△ABC中，AB=4，BC=3，点P在边BC上沿B→C运动，则△ABP的面积小于4的概率为
 
．
若x，y满足约束条件
x+y≤3
y≤x+1
x+3y≥3
，则函数z=2x-y的最大值是（　　）
A、-1B、0C、3D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网