题目内容
在一条笔直的工艺流水线上有n个工作台,将工艺流水线用如图所示的数轴表示,各工作台的坐标分别为x1,x2,…,xn,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
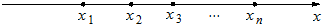
(Ⅰ)若n=2,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若n=5,工作台从左到右的人数依次为3,2,1,2,2,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
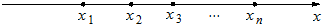
(Ⅰ)若n=2,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若n=5,工作台从左到右的人数依次为3,2,1,2,2,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
考点:分段函数的应用,绝对值不等式
专题:函数的性质及应用
分析:(Ⅰ)若n=2,根据条件建立d(x)的关系式,即可确定供应站的位置;
(Ⅱ)若n=5,根据条件建立d(x)的关系式,即可确定供应站的位置.
(Ⅱ)若n=5,根据条件建立d(x)的关系式,即可确定供应站的位置.
解答:
解:设供应站坐标为x,各工作台上的所有工人到供应站的距离之和为d(x).
(Ⅰ)d(x)=|x-x1|+|x-x2|=
,
当x<x1时,d(x)=-2x+(x1+x2)在区间(-∞,x1)上是减函数;
当x>x2时,d(x)=2x-(x1+x2)在区间(x2,+∞)上是增函数.
则当x∈[x1,x2]时,d(x)=x2-x1式取最小值,即供应站的位置为[x1.x2]内的任意一点.
(Ⅱ)由题设知,各工作台上的所有工人到供应站的距离之和为d(x)=3|x-x1|+2|x-x2|+|x-x3|+2|x-x4|+2|x-x5|,
类似于(Ⅰ)的讨论知,x1≤x≤x5,且有d(x)=
,
所以,函数d(x)在区间(x1,x2)上是减函数,在区间(x3,x5)上是增函数,在区间[x2,x3]上是常数.
故供应站位置位于区间[x2,x3]上任意一点时,均能使函数d(x)取得最小值,且最小值为x3+2x4+2x3-3x1-2x2,x2≤x≤x3.
(Ⅰ)d(x)=|x-x1|+|x-x2|=
|
当x<x1时,d(x)=-2x+(x1+x2)在区间(-∞,x1)上是减函数;
当x>x2时,d(x)=2x-(x1+x2)在区间(x2,+∞)上是增函数.
则当x∈[x1,x2]时,d(x)=x2-x1式取最小值,即供应站的位置为[x1.x2]内的任意一点.
(Ⅱ)由题设知,各工作台上的所有工人到供应站的距离之和为d(x)=3|x-x1|+2|x-x2|+|x-x3|+2|x-x4|+2|x-x5|,
类似于(Ⅰ)的讨论知,x1≤x≤x5,且有d(x)=
|
所以,函数d(x)在区间(x1,x2)上是减函数,在区间(x3,x5)上是增函数,在区间[x2,x3]上是常数.
故供应站位置位于区间[x2,x3]上任意一点时,均能使函数d(x)取得最小值,且最小值为x3+2x4+2x3-3x1-2x2,x2≤x≤x3.
点评:本题主要考查分段函数的最值的计算,综合性较强,难度较大.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
设(2+i)
=3+4i,则z=( )
. |
| z |
| A、1+2i | B、1-2i |
| C、2+i | D、2-i |
设点P(x,y),其中x,y∈N,则满足x+y≤3的点P的个数为( )
| A、10 | B、9 | C、3 | D、无数 |
在区间[0,4]内随机取两个实数a,b,则使得方程x2+ax+b2=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知椭圆
如图,已知椭圆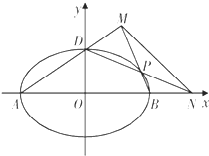 已知椭圆
已知椭圆