题目内容
在边长为2的正方形ABCD内随机取一点M,则AM<1的概率为 .
考点:几何概型
专题:概率与统计
分析:由扇形面积公式,结合题意算出满足条件的点E对应的图形的面积,求出正方体ABCD的面积并利用几何概型计算公式,即可算出所求概率.
解答:
 解:当点E满足AE<1时,E在以A为圆心、半径为1的圆内
解:当点E满足AE<1时,E在以A为圆心、半径为1的圆内
其在边长为2的正方形ABCD内面积为
π×12=
∵正方形ABCD边长为2,得正方形的面积为S=22=4
∴所求概率为P=
=
=
.
故答案为:
.
 解:当点E满足AE<1时,E在以A为圆心、半径为1的圆内
解:当点E满足AE<1时,E在以A为圆心、半径为1的圆内其在边长为2的正方形ABCD内面积为
| 1 |
| 4 |
| π |
| 4 |
∵正方形ABCD边长为2,得正方形的面积为S=22=4
∴所求概率为P=
| S′ |
| S |
| ||
| 4 |
| π |
| 16 |
故答案为:
| π |
| 16 |
点评:本题在正方形中求点E满足条件的概率,着重考查了扇形面积、正方形面积计算公式和几何概型计算公式等知识,属于基础题.

练习册系列答案
相关题目
球面上有M、N两点,在过M、N的球的大圆上,
的度数为90°,在过M、N的球小圆上,
的度数为120°,又MN=
cm,则球心到上述球小圆的距离是( )
 |
| MN |
 |
| MN |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
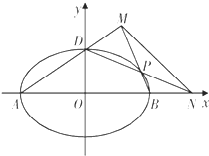 已知椭圆
已知椭圆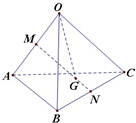 已知空间四边形OABC,其对角线为OB,AC,M,N分别是边OA,BC的中点,点G在线段MN上,若MG=λGN,且
已知空间四边形OABC,其对角线为OB,AC,M,N分别是边OA,BC的中点,点G在线段MN上,若MG=λGN,且