题目内容
已知
=(y-m,sinx),
=(1,sinx-1).
⊥
(1)求y关于x的函数关系式y=f(x);
(2)若y=f(x)的图象无零点,求m的取值范围;
(3)求y=f(x)的单调递增区间.
| a |
| b |
| a |
| b |
(1)求y关于x的函数关系式y=f(x);
(2)若y=f(x)的图象无零点,求m的取值范围;
(3)求y=f(x)的单调递增区间.
考点:平面向量数量积的运算,函数零点的判定定理
专题:平面向量及应用
分析:(1)利用向量垂直与数量积的关系即可得出;
(2)利用sinx的值域即可得出;
(3)令t=sinx,则y=-t2+t+m=-(t-
)2+
+m,利用二次函数的单调性与y=sinx的单调性即可得出.
(2)利用sinx的值域即可得出;
(3)令t=sinx,则y=-t2+t+m=-(t-
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:(1)∵
⊥
,∴y-m+sinx(sinx-1)=0,
∴y=f(x)=-sinx2+sinx+m,x∈R.
(2)∵sinx∈[-1,1],
∴y=f(x)∈[-2+m,
+m];
若y=f(x)的图象无零点,则-2+m>0或
+m<0,
解得m>2或m<-
.
(3)令t=sinx,则y=-t2+t+m=-(t-
)2+
+m,
当t>0.5时,y=-t2+t+m是单调递减的,
此时t=sinx的递减区间[2kπ+
,2kπ+
];
当t<0.5时,y=-t2+t+m是单调递增的,
且此时t=sinx的递增区间[2kπ-
,2kπ+
];
综上,由复合函数单调性判定法则得所求函数的单调递增区间:[2kπ+
,2kπ+
];和[2kπ-
,2kπ+
];k∈Z.
| a |
| b |
∴y=f(x)=-sinx2+sinx+m,x∈R.
(2)∵sinx∈[-1,1],
∴y=f(x)∈[-2+m,
| 1 |
| 4 |
若y=f(x)的图象无零点,则-2+m>0或
| 1 |
| 4 |
解得m>2或m<-
| 1 |
| 4 |
(3)令t=sinx,则y=-t2+t+m=-(t-
| 1 |
| 2 |
| 1 |
| 4 |
当t>0.5时,y=-t2+t+m是单调递减的,
此时t=sinx的递减区间[2kπ+
| π |
| 2 |
| 5π |
| 6 |
当t<0.5时,y=-t2+t+m是单调递增的,
且此时t=sinx的递增区间[2kπ-
| π |
| 2 |
| π |
| 6 |
综上,由复合函数单调性判定法则得所求函数的单调递增区间:[2kπ+
| π |
| 2 |
| 5π |
| 6 |
| π |
| 2 |
| π |
| 6 |
点评:本题考查了数量积运算与垂直的关系、二次函数的单调性、正弦函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
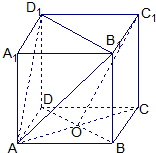 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.