题目内容
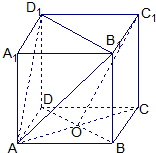已知正方体ABCD-A1B1C1D1，O是底ABCD对角线的交点．求证：
（1）A1C⊥B1D1
（2）C1O∥面AB1D1．
考点：直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：（1）可由正方形的性质得到A1C1⊥B1D1，再由线面垂直的性质得到A1A⊥B1D1，由线面垂直的判定定理得到B1D1⊥平面A1ACC1，再由性质即可得证；
（2）连接A1C1交B1D1于O1，连接AO1，证得四边形OCC1O1是平行四边形，即AO1∥OC1，再由线面平行的判定定理，即可得证．
（2）连接A1C1交B1D1于O1，连接AO1，证得四边形OCC1O1是平行四边形，即AO1∥OC1，再由线面平行的判定定理，即可得证．
解答：
证明：（1）由ABCD-A1B1C1D1是正方体，所以A1C1⊥B1D1，
又A1A⊥平面A1B1C1D1，所以A1A⊥B1D1
又AA1∩A1C1=A1，
由线面垂直的判定定理，有B1D1⊥平面A1ACC1，
而A1C?平面A1ACC1，
所以A1C⊥B1D1；
（2）连接A1C1交B1D1于O1，连接AO1，
由ABCD-A1B1C1D1是正方体，所以AC∥A1C1，且O1C1=AO=
AC，
即四边形OCC1O1是平行四边形，
所以AO1∥OC1，
又AO1?平面AB1D1，OC1?平面AB1D1，
则C1O∥面AB1D1．
证明：（1）由ABCD-A1B1C1D1是正方体，所以A1C1⊥B1D1，又A1A⊥平面A1B1C1D1，所以A1A⊥B1D1
又AA1∩A1C1=A1，
由线面垂直的判定定理，有B1D1⊥平面A1ACC1，
而A1C?平面A1ACC1，
所以A1C⊥B1D1；
（2）连接A1C1交B1D1于O1，连接AO1，
由ABCD-A1B1C1D1是正方体，所以AC∥A1C1，且O1C1=AO=
| 1 |
| 2 |
即四边形OCC1O1是平行四边形，
所以AO1∥OC1，
又AO1?平面AB1D1，OC1?平面AB1D1，
则C1O∥面AB1D1．
点评：本题考查空间直线与平面的位置关系：平行和垂直．考查线面平行和垂直的判定和性质定理的运用，考查空间想象能力，属于中档题．
练习册系列答案
相关题目
若复数z=
的共轭复数为（ ）
| 2+i |
| 1+i |
A、
| ||
B、
| ||
C、
| ||
D、
|