题目内容
A,B,C,D是棱长为4的正方体的四个顶点,且三棱锥A-BCD的四个面都是直角三角形,则其全面积为 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:作出图形,由此得到S△ABC=S△BCD=
×4×4=8,S△ACD=S△ABD=
×
×4=8
,由此能求出三棱锥A-BCD的全面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 4+4 |
| 2 |
解答:
解:如图,A,B,C,D是棱长为4的正方体的四个顶点,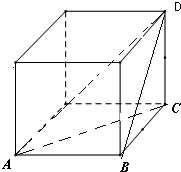
且三棱锥A-BCD的四个面都是直角三角形,
∴S△ABC=S△BCD=
×4×4=8,
S△ACD=S△ABD=
×
×4=8
,
∴三棱锥A-BCD的全面积:
S=8+8+8
+8
=16+16
.
故答案为:16+16
.

且三棱锥A-BCD的四个面都是直角三角形,
∴S△ABC=S△BCD=
| 1 |
| 2 |
S△ACD=S△ABD=
| 1 |
| 2 |
| 4+4 |
| 2 |
∴三棱锥A-BCD的全面积:
S=8+8+8
| 2 |
| 2 |
| 2 |
故答案为:16+16
| 2 |
点评:本题考查三棱锥A-BCD的全面积的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
一条直线的倾斜角的正弦值为
,则此直线的斜率是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、±
|
函数f(x)的导函数为f′(x),对?x∈R,都有f′(x)>f(x)成立,若f(ln2)=2,则不等式f(x)>ex的解是( )
| A、x>1 |
| B、0<x<1 |
| C、x>ln2 |
| D、0<x<ln2 |
若复数z=
的共轭复数为( )
| 2+i |
| 1+i |
A、
| ||
B、
| ||
C、
| ||
D、
|
设等差数列{an}的前n项和为Sn,已知(a2012-1)3+2014a2012=0,a33-3a32+2017a3=4029,则下列结论正确的是( )
| A、S2014=2014,a2012<a3 |
| B、S2014=2014,a2012>a3 |
| C、S2014=2013,a2012<a3 |
| D、S2014=2013,a2012>a3 |