题目内容
已知数列{an}满足a1=2，an=2an-1+2 n+1
（1）若bn=
，求证{bn}为等差数列；
（2）求{an}的通项公式．
（1）若bn=
| an |
| 2n |
（2）求{an}的通项公式．
考点：数列递推式,等差关系的确定
专题：等差数列与等比数列
分析：（1）把已知数列递推式两边同时除以2n，移向后即可证得{bn}为等差数列；
（2）由等差数列的通项公式求得{bn}的通项公式，则{an}的通项公式可求．
（2）由等差数列的通项公式求得{bn}的通项公式，则{an}的通项公式可求．
解答：
（1）证明：由an=2an-1+2 n+1，得
-
=2（n≥2），
∵bn=
，
∴bn-bn-1=2，
∴{bn}为等差数列；
（2）解：∵{bn}为等差数列，
且b1=
=1，
∴bn=b1+（n-1）d=1+2（n-1）=2n-1，
即
=2n-1，
∴an=(2n-1)2n．
| an |
| 2n |
| an-1 |
| 2n-1 |
∵bn=
| an |
| 2n |
∴bn-bn-1=2，
∴{bn}为等差数列；
（2）解：∵{bn}为等差数列，
且b1=
| a1 |
| 2 |
∴bn=b1+（n-1）d=1+2（n-1）=2n-1，
即
| an |
| 2n |
∴an=(2n-1)2n．
点评：本题考查了数列递推式，考查了等差关系的确定，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
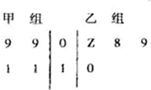如图茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以Z表示．