题目内容
已知(
-
)n的展开式的各项系数之和等于(4
-
)5展开式中的常数项,求(
-
)n展开式中含x-1的项的二项式系数.
| 3 | ||
|
| 3 | x |
| 3 | x |
| 1 | ||
|
| 3 | ||
|
| 3 | x |
考点:二项式定理的应用
专题:二项式定理
分析:先求得 (4
-
)5展开式中的常数项为 T3=27,而(
-
)n的展开式各项系数和为27,结合条件求得n=7,由(
-
)7的二项展开式的通项公式知,含x-1的项是第4项(r=3),从而求得该项的二项式系数.
| 3 | x |
| 1 | ||
|
| 3 | ||
|
| 3 | x |
| 3 | ||
|
| 3 | x |
解答:
解:由于 (4
-
)5的展开式的通项为Tr+1=
(4
)5-r(-
)r=(-
)r•45-r
•x
,(r=0,1,2,3,4,5),
若它为常数项,则
=0,求得r=2,代入上式求得常数项为 T3=27.
即常数项是27,从而可得(
-
)n的展开式各项系数和为2n=27,∴n=7.
同理(
-
)7由二项展开式的通项公式知,含x-1的项是第4项(r=3),
其二项式系数是
=35.
| 3 | x |
| 1 | ||
|
| C | r 5 |
| 3 | x |
| 1 | ||
|
| 1 | ||
|
| C | r 5 |
| 10-5r |
| 6 |
若它为常数项,则
| 10-5r |
| 6 |
即常数项是27,从而可得(
| 3 | ||
|
| 3 | x |
同理(
| 3 | ||
|
| 3 | x |
其二项式系数是
| C | 2 7 |
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn,已知(a2012-1)3+2014a2012=0,a33-3a32+2017a3=4029,则下列结论正确的是( )
| A、S2014=2014,a2012<a3 |
| B、S2014=2014,a2012>a3 |
| C、S2014=2013,a2012<a3 |
| D、S2014=2013,a2012>a3 |
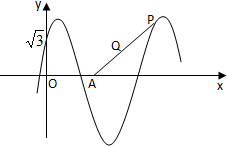 如图所示,函数y=2sin(ωx+ϕ)(x∈R,ω>0,0≤ϕ≤
如图所示,函数y=2sin(ωx+ϕ)(x∈R,ω>0,0≤ϕ≤