题目内容
已知双曲线
-
=1上点P到右焦点的距离为14，则其到左焦点距离（ ）
| x2 |
| 64 |
| y2 |
| 36 |
| A、30 | B、30或2 |
| C、6或22 | D、22 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据双曲线的定义，判断点P的位置即可得到结论．
解答：
解：友双曲线方程可知a=8，c=10，
若点P位于双曲线的左支，则P到右焦点的距离d≥a+c=18此时14≥18不成立．
故点P位于双曲线的右支，
设到到左焦点距离为d，
则d-14=2a=16，
则d=14+16=30，
故选：A．
若点P位于双曲线的左支，则P到右焦点的距离d≥a+c=18此时14≥18不成立．
故点P位于双曲线的右支，
设到到左焦点距离为d，
则d-14=2a=16，
则d=14+16=30，
故选：A．
点评：本题主要考查双曲线的定义，判断P的位置是解决本题的关键．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
一个正三棱柱的三视图如图所示，则这个正三棱柱的高和底面边长分别为（ ）
A、1，
| ||
B、
| ||
| C、2，1 | ||
| D、1，2 |
如果命题“￢（p∧q）”为假命题，则（ ）
| A、p、q均为真命题 |
| B、p、q均为假命题 |
| C、p、q至少有一个为真命题 |
| D、p、q至多有一个为真命题 |
观察下面的演绎推理过程，判断正确的是（ ）
大前提：若直线a⊥直线 l，且直线b⊥直线 l，则a∥b．
小前提：正方体 ABCD-A1B1C1D1中，A1B1⊥AA1．且AD⊥AA1
结论：A1B1∥AD．
大前提：若直线a⊥直线 l，且直线b⊥直线 l，则a∥b．
小前提：正方体 ABCD-A1B1C1D1中，A1B1⊥AA1．且AD⊥AA1
结论：A1B1∥AD．
| A、推理正确 |
| B、大前提出错导致推理错误 |
| C、小前提出错导致推理错误 |
| D、仅结论错误 |
已知一个60°的二面角的棱上有两点A，B，AC，BD分别是在这个二面角的两个面内垂直于AB的线段，若AB=4，AC=6，BD=8，则CD=（ ）
A、2
| ||
B、2
| ||
C、2
| ||
| D、10 |
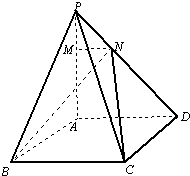已知四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD，∠BAD=120°，PA=AB=2