题目内容
观察下面的演绎推理过程，判断正确的是（ ）
大前提：若直线a⊥直线 l，且直线b⊥直线 l，则a∥b．
小前提：正方体 ABCD-A1B1C1D1中，A1B1⊥AA1．且AD⊥AA1
结论：A1B1∥AD．
大前提：若直线a⊥直线 l，且直线b⊥直线 l，则a∥b．
小前提：正方体 ABCD-A1B1C1D1中，A1B1⊥AA1．且AD⊥AA1
结论：A1B1∥AD．
| A、推理正确 |
| B、大前提出错导致推理错误 |
| C、小前提出错导致推理错误 |
| D、仅结论错误 |
考点：演绎推理的意义
专题：规律型
分析：本题考查的知识点是演绎推理的基本方法及整数的，在使用三段论推理证明中，如果命题是错误的，则可能是“大前提”错误，也可能是“小前提”错误，也可能是推理形式错误，根据“若直线a⊥直线 l，且直线b⊥直线 l，此时a，b可能平行，可能异面，也可能相交，可知：已知前提错误．
解答：
解：∵若直线a⊥直线 l，且直线b⊥直线 l，此时a，b可能平行，可能异面，也可能相交，
∴大前提：若直线a⊥直线 l，且直线b⊥直线 l，则a∥b错误，
故这个推理过程中，大前提出错导致推理错误，
故选：B
∴大前提：若直线a⊥直线 l，且直线b⊥直线 l，则a∥b错误，
故这个推理过程中，大前提出错导致推理错误，
故选：B
点评：演绎推理的主要形式就是由大前提、小前提推出结论的三段论推理．三段论推理的依据用集合论的观点来讲就是：若集合M的所有元素都具有性质P，S是M的子集，那么S中所有元素都具有性质P．三段论的公式中包含三个判断：第一个判断称为大前提，它提供了一个一般的原理；第二个判断叫小前提，它指出了一个特殊情况；这两个判断联合起来，揭示了一般原理和特殊情况的内在联系，从而产生了第三个判断结论．演绎推理是一种必然性推理，演绎推理的前提与结论之间有蕴涵关系．因而，只要前提是真实的，推理的形式是正确的，那么结论必定是真实的，但错误的前提可能导致错误的结论．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
如图所示，P、Q分别在BC和AC上，BP：CP=2：5，CQ：QA=3：4，则
（ ）
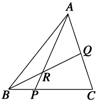
| AR |
| RP |
| A、3：14 | B、14：3 |
| C、17：3 | D、17：14 |
下面是一段“三段论”推理过程：若函数f（x）在（a，b）内可导且单调递增，则在（a，b）内，f′（x）＞0恒成立．因为f（x）=x3在（-1，1）内可导且单调递增，所以在（-1，1）内，f′（x）=3x2＞0恒成立．以上推理中（ ）
| A、大前提错误 |
| B、小前提错误 |
| C、结论正确 |
| D、推理形式错误 |
若点P为双曲线
-
=1（a＞0，b＞0）上任意一点，过点P作双曲线两渐近线的平行线，分别与两渐近线交于M，N两点，若|PM|•|PN|=b2，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线
-
=1上点P到右焦点的距离为14，则其到左焦点距离（ ）
| x2 |
| 64 |
| y2 |
| 36 |
| A、30 | B、30或2 |
| C、6或22 | D、22 |
如图，在四棱锥P-ABCD中，PD⊥面ABCD，AB∥DC，AB⊥AD，E为AB的中点，AB=8，AD=DC=4，∠PAD=60°．