题目内容
定义在R上的函数f(x)=f(4-x),且f(2-x)+f(x-2)=0,求f(2012)的值.
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:将等式f (2-x)+f (x-2)=0的x用x+2代替得到函数为奇函数;利用奇函数化简等式f(x)=f (4-x);得到函数是周期函数,利用函数的周期求出f(2012).
解答:
解:∵f (2-x)+f (x-2)=0
∴f(x-2)=-f(2-x)
将x用x+2代替得到f(x)=-f(-x)
∴f(x)为奇函数
∵f(x)=f (4-x)
f(x)=-f(x-4)
将x用x+4代替得f(x+4)=-f(x)
∴f(x+4)=f(x-4)
∴函数以8为周期
∴f(2012)=f(4)=f(0)=0.
∴f(x-2)=-f(2-x)
将x用x+2代替得到f(x)=-f(-x)
∴f(x)为奇函数
∵f(x)=f (4-x)
f(x)=-f(x-4)
将x用x+4代替得f(x+4)=-f(x)
∴f(x+4)=f(x-4)
∴函数以8为周期
∴f(2012)=f(4)=f(0)=0.
点评:本题考查对于抽象函数常通过给已知等式中的自变量赋值得到新等式,研究出函数的性质.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-3)到焦点的距离等于5,则m等于( )
A、2
| ||
| B、±2 | ||
C、±
| ||
D、±2
|
已知双曲线
-
=1上点P到右焦点的距离为14,则其到左焦点距离( )
| x2 |
| 64 |
| y2 |
| 36 |
| A、30 | B、30或2 |
| C、6或22 | D、22 |
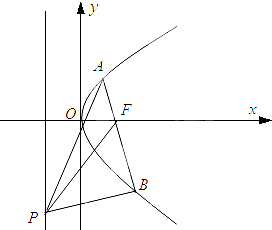 已知抛物线y2=2px(p>0)上点M(3,m)到焦点F的距离为4.
已知抛物线y2=2px(p>0)上点M(3,m)到焦点F的距离为4.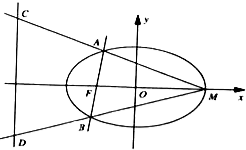 已知椭圆
已知椭圆 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.