题目内容
一个正三棱柱的三视图如图所示,则这个正三棱柱的高和底面边长分别为( )


A、1,
| ||
B、
| ||
| C、2,1 | ||
| D、1,2 |
考点:由三视图求面积、体积
专题:常规题型
分析:解:先想象正三棱柱的形状及摆放的位置,再画出其直观图,即可得此正三棱柱的高和底面边长.
解答:
解:由三视图画出几何体的直观图,如右图所示.
根据侧视图的宽为几何体的高,可知正三棱柱的高为1.
根据侧视图的长为几何体的宽,可知正三棱柱底面三角形的高为
,
从而底面边AB的长为
=
=2,
故选D.

根据侧视图的宽为几何体的高,可知正三棱柱的高为1.
根据侧视图的长为几何体的宽,可知正三棱柱底面三角形的高为
| 3 |
从而底面边AB的长为
| BD |
| sin∠BAD |
| ||
| sin60° |
故选D.
点评:本题是根据三视图想象几何体的形状,考查了学生的空间想象能力.关键是:
(1)弄清几何体的上、下、左、右、前、后方位;
(2)理清三视图的边长与原几何体的长、宽、高的联系,即正视图与俯视图等长,正视图与侧视图等高,侧视图与俯视图等宽.
(1)弄清几何体的上、下、左、右、前、后方位;
(2)理清三视图的边长与原几何体的长、宽、高的联系,即正视图与俯视图等长,正视图与侧视图等高,侧视图与俯视图等宽.

练习册系列答案
相关题目
已知θ是直线y=2x的倾斜角,则cosθ=( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知抛物线的顶点在原点,焦点在y轴上,抛物线上的点P(m,-3)到焦点的距离等于5,则m等于( )
A、2
| ||
| B、±2 | ||
C、±
| ||
D、±2
|
如图所示,P、Q分别在BC和AC上,BP:CP=2:5,CQ:QA=3:4,则
( )
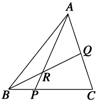
| AR |
| RP |

| A、3:14 | B、14:3 |
| C、17:3 | D、17:14 |
若集合M=(y|y=x2-2x+1},N={x|y=x+
+2},则M与N的关系是( )
| 2x |
| A、M=N | B、M≠N |
| C、M∈N | D、M⊆N |
下面是一段“三段论”推理过程:若函数f(x)在(a,b)内可导且单调递增,则在(a,b)内,f′(x)>0恒成立.因为f(x)=x3在(-1,1)内可导且单调递增,所以在(-1,1)内,f′(x)=3x2>0恒成立.以上推理中( )
| A、大前提错误 |
| B、小前提错误 |
| C、结论正确 |
| D、推理形式错误 |
已知双曲线
-
=1上点P到右焦点的距离为14,则其到左焦点距离( )
| x2 |
| 64 |
| y2 |
| 36 |
| A、30 | B、30或2 |
| C、6或22 | D、22 |
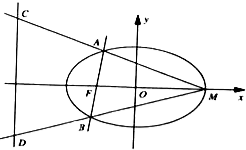 已知椭圆
已知椭圆