题目内容
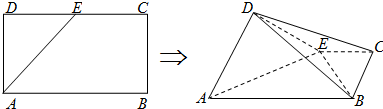
如图所示,在长方形ABCD中,AB=2BC,E为CD的中点.将△AED沿AE折起,使平面ADE⊥平面ABCE,连接DB、DC、EB.
(1)求证:CE∥平面ABD;
(2)求证:平面ABD⊥平面BDE.
(1)求证:CE∥平面ABD;
(2)求证:平面ABD⊥平面BDE.

考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)先证明出CE∥AB,进而根据线面平行的判定定理证明出CE∥平面ABD
(2)过点D在平面ADE内作DM⊥AE,证明出DM⊥平面ABCE,根据线面垂直的性质得知BE⊥DM,进而证明出BE⊥平面ADE.进一步证明出BE⊥AD,根据线面垂直的判定证明出
AD⊥平面BDE,最后根据线面垂直的判定定理证明出平面ABD⊥平面BDE.
(2)过点D在平面ADE内作DM⊥AE,证明出DM⊥平面ABCE,根据线面垂直的性质得知BE⊥DM,进而证明出BE⊥平面ADE.进一步证明出BE⊥AD,根据线面垂直的判定证明出
AD⊥平面BDE,最后根据线面垂直的判定定理证明出平面ABD⊥平面BDE.
解答:
证明:(1)在长方形ABCD中,CE∥AB,
又AB?平面ABD,CD?平面ABD,
∴CE∥平面ABD
(2)过点D在平面ADE内作DM⊥AE,
∵平面ADE⊥平面ABCE,平面ADE∩平面ABCE=AE,
∴DM⊥平面ABCE,
∵BE?平面ABCE,所以BE⊥DM,
又∵BE⊥AE,DM∩AE=M,即BE⊥平面ADE.
∵AD?平面ADE,
∴BE⊥AD.
又∵AD⊥DE,BE∩DE=E,
∴AD⊥平面BDE,
又∵AD?平面ABD,
∴平面ABD⊥平面BDE.
又AB?平面ABD,CD?平面ABD,
∴CE∥平面ABD
(2)过点D在平面ADE内作DM⊥AE,
∵平面ADE⊥平面ABCE,平面ADE∩平面ABCE=AE,
∴DM⊥平面ABCE,

∵BE?平面ABCE,所以BE⊥DM,
又∵BE⊥AE,DM∩AE=M,即BE⊥平面ADE.
∵AD?平面ADE,
∴BE⊥AD.
又∵AD⊥DE,BE∩DE=E,
∴AD⊥平面BDE,
又∵AD?平面ABD,
∴平面ABD⊥平面BDE.
点评:本题主要考查了线面平行,线面垂直,面面垂直的判定.注重了对学生逻辑思维能力和空间观察能力的考查.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知双曲线
-
=1上点P到右焦点的距离为14,则其到左焦点距离( )
| x2 |
| 64 |
| y2 |
| 36 |
| A、30 | B、30或2 |
| C、6或22 | D、22 |
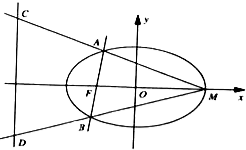 已知椭圆
已知椭圆 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,E为AB的中点,AB=8,AD=DC=4,∠PAD=60°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,E为AB的中点,AB=8,AD=DC=4,∠PAD=60°.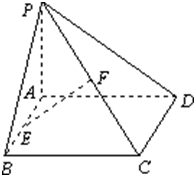 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD. 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.