题目内容

已知一个60°的二面角的棱上有两点A，B，AC，BD分别是在这个二面角的两个面内垂直于AB的线段，若AB=4，AC=6，BD=8，则CD=（　　）
A、2
41
B、2
3
C、2
17
D、10
考点：与二面角有关的立体几何综合题
专题：综合题,空间位置关系与距离
分析：由已知可得
CD
=
CA
+
AB
+
BD
，利用数量积的性质即可得出．
解答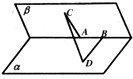： 解：∵CA⊥AB，BD⊥AB，∴
CA
•
AB
=
BD
•
AB
=0，
∵＜
AC
，
BD
＞=60°，∴＜
CA
，
BD
＞=120°．
∵
CD
=
CA
+
AB
+
BD
，
∴
CD
2=
CA
2+
AB
2+
BD
2+2
CA
•
AB
+2
CA
•
BD
+2
AB
•
BD

=62+42+82+0+2×6×8×cos120°+0
=68．
∴|
CD
|=2
17
．
故选：C．
点评：熟练掌握向量的运算和数量积运算是解题的关键．
练习册系列答案
相关题目
棱长为4的正方体内切球的表面积为（　　）
A、4πB、16π
C、8πD、12π
若集合M=（y|y=x2-2x+1}，N={x|y=x+
2x
+2}，则M与N的关系是（　　）
A、M=NB、M≠N
C、M∈ND、M⊆N
若将集合A中的数按从小到大排成数列{an}，则有a1=31+2×0=3，a2=32+2×0=9，a3=32+2×1=11，a4=33+2×0=27，…，依此类推，将数列依次排成如图所示的三角形数阵，则第六行第三个数为（　　）
A、247B、735
C、731D、733
已知双曲线
x2
64
-
y2
36
=1上点P到右焦点的距离为14，则其到左焦点距离（　　）
A、30B、30或2
C、6或22D、22
数列{an}满足a1=
5
2
，an+1=
5an-8
2an-3
（n∈N*），bn=
1
an-2

（Ⅰ）证明：数列{bn}为等差数列；
（Ⅱ）已知cn=bn（-
9
10
）n，求数列{cn}的最大项为第几项；
（Ⅲ）设Sn为{bn}的前n项和，dn=[
Sn
n+4
]，其中[x]为不超过x的最大整数，求数列{dn}的前n项和Tn．
已知抛物线y2=2px（p＞0）上点M（3，m）到焦点F的距离为4．
（Ⅰ）求抛物线方程；
（Ⅱ）点P为准线上任意一点，AB为抛物线上过焦点的任意一条弦，设直线PA，PB，PF的斜率为k1，k2，k3，问是否存在实数λ，使得k1+k2=λk3恒成立．若存在，请求出λ的值；若不存在，请说明理由．
已知椭圆C的焦点坐标分别为（
3
，0）（-
3
，0），长轴是短轴的两倍． 
（1）求椭圆C的方程； 
（2）在y的正半轴上是否存在一点P（0，p），过定点P作任意一条直线与椭圆C交于两点S，T，使得
OS
•
OT
为一个定值．若存在，请求出点P的坐标，若不存在，请说明理由．
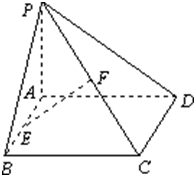已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、PC的中点，且PA=AD．
（1）求证：EF∥平面PAD；
（2）求证：面PEC⊥面PCD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网