Question

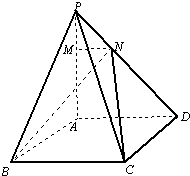已知四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD，∠BAD=120°，PA=AB=2

2

，点N在线段PD上，且PN=kPD（0＜k＜1），平面BCN与PA相交于点M，
（Ⅰ）求证：AD∥MN；
（Ⅱ）试确定点N的位置． 使直线BN与平面PAD所成角的正切值为

6

3

．

Answer 1

考点：直线与平面所成的角

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）证明AD∥MN，只需证明AD∥平面BCN；
（Ⅱ）延长DA，过B作BQ⊥AD于Q，连接QN得∠BNQ即直线BN与平面PAD所成的角，求出BQ，QN，即可确定点N的位置．

解答： （Ⅰ）证明：∵AD∥BC，BC?平面BCN，AD?平面BCN，
∴AD∥平面BCN，…（3分）
又AD?平面PAD，平面PAD∩平面BCN=MN，
∴AD∥MN…（5分）
（Ⅱ）解：延长DA，过B作BQ⊥AD于Q，
∵PA⊥底面ABCD，∴PA⊥BQ，从而BQ⊥平面PAD，
连接QN得∠BNQ即直线BN与平面PAD所成的角，…（7分）
∵PD=4，底面ABCD为菱形且∠BAD=120°，∴AQ=

1

2

AB=

1

2

AD=

2

，BQ=

6

，
∴QD=3

2

，PN=kPD=4k，
∴ND=4-4k，
∴△QDN中，QN=

QD2+ND2-2QD•NDcos45°

=

(3 2 )2+(4-4k)2-2×3 2 ×(4-4k)× 2 2

=

16k2-8k+10

，（11分）
∴tan∠BNQ=

BQ

QN

=

6

QN

=

6

3

，
∴QN=3，从而k=

1

4

，
答：点N位于的线段PD的四分之一处（靠近P点）…（14分）

点评：本题考查线面平行的判定与性质，考查线面角，正确运用线面平行的判定定理是关键．