题目内容

设f（n）=2+24+27+210+…+23n+10（n∈N），则f（n）等于（　　）
A、
2
7
（8n-1）
B、
2
7
（8n+1-1）
C、
2
7
（8n+3-1）
D、
2
7
（8n+4-1）
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：利用等比数列的前n项和公式即可得出．
解答： 解：f（n）=2+24+27+210+213+215+…+23n+10
=
2×[(23)n+4-1]
23-1

=
2
7
(8n+4-1)．
故选：D．
点评：本题考查了等比数列的前n项和公式，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
ex
a
-
a
ex
，（a∈R且a＞0）．
（1）判断函数f（x）的单调性，并证明；
（2）若函数f（x）的定义域为（-2，2）时，求使f（1-m）-f（m2-1）＜0成立的实数m的取值范围．
已知f（x）是定义在R上的奇函数，且对任意实数x∈R均有f（x-1）=f（x+1），当x∈[0，1）时，f（x）=2x-1，则f（log
1
2
6）=
 
．
如图为一个四棱锥的正视图、侧（左）视图和俯视图，则该四棱锥的表面积为（　　）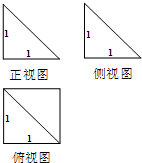
A、3
B、2+
2
C、2
D、3+2
2
已知函数f（x）=sin（ωx-
π
6
）（ω＞0）在（0，
4π
3
）上单调递增，则ω的最大值为（　　）
A、
1
2
B、
3
4
C、1
D、
3
2
“a≤0”是“函数f（x）=|（ax-1）x|在区间（0，+∞）内单调递增”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
在平面直角坐标系，动点P（x，y）在第一象限且点P到点（1，1）的距离等于点P到两坐标轴距离之和，则x2+y2的最小值为
 
．
函数f（x）=-x2-4x+1（-3≤x≤3）的值域是（　　）
A、（-4，5]
B、[-20，4]
C、[-20，5]
D、[4，5]
函数f（x）=cosx-
3
sinx的一条对称轴方程是（　　）
A、x=
π
6
B、x=
π
3
C、x=-
π
3
D、x=
π
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网