题目内容
11.f(x)=2sin(πx$-\frac{π}{4}$)+$\frac{1}{sin(πx-\frac{π}{4})}$=a在($\frac{1}{4}$,1]上有且只有两个解,则a的值为2$\sqrt{2}$.分析 利用换元法结合三角函数的性质求出t的取值范围,利用对勾函数的性质建立方程即可得到结论.
解答 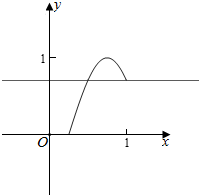 解:设t=sin(πx$-\frac{π}{4}$),
解:设t=sin(πx$-\frac{π}{4}$),
∵x∈($\frac{1}{4}$,1],
∴πx∈($\frac{π}{4}$,π],πx-$\frac{π}{4}$∈(0,$\frac{3π}{4}$],
则t=sin(πx$-\frac{π}{4}$)∈(0,1],
且当0<t<$\frac{\sqrt{2}}{2}$或t=1时,方程t=sin(πx$-\frac{π}{4}$)有一解,
当$\frac{\sqrt{2}}{2}$≤t<1时,方程t=sin(πx$-\frac{π}{4}$)有2解,
则y=2t+$\frac{1}{t}$=2(t+$\frac{\frac{1}{2}}{t}$),则函数在(0,$\frac{\sqrt{2}}{2}$)上递减,在($\frac{\sqrt{2}}{2}$,1]上递增,
故当t=$\frac{\sqrt{2}}{2}$时,函数y=2t+$\frac{1}{t}$=2(t+$\frac{\frac{1}{2}}{t}$)有一个解,此时y=2$\sqrt{2}$,
故a=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题主要考查根的个数的判断,利用换元法结合三角函数和对勾函数的图象和性质是解决本题的关键.综合性较强.

练习册系列答案
相关题目
2.若$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(4,k),$\overrightarrow{c}$=$\overrightarrow{0}$,则($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=( )
| A. | 0 | B. | $\overrightarrow{0}$ | C. | 4+2k | D. | 8+k |
19.已知数列$\frac{1}{1×2},\frac{1}{2×3},\frac{1}{3×4},…,\frac{1}{{n×({n+1})}},…$,下面各数中是此数列中的项的是( )
| A. | $\frac{1}{35}$ | B. | $\frac{1}{42}$ | C. | $\frac{1}{48}$ | D. | $\frac{1}{54}$ |
 如图所示,在正方体ABCD-A1B1C1D1中,
如图所示,在正方体ABCD-A1B1C1D1中,