题目内容
7.求实数m的值,使复数(m2-2m-3)+(m2-3m-4)i分别是:(1)实数;
(2)纯虚数;
(3)零.
分析 分别由实部和虚部为0求得m值,然后逐一结合复数为实数、纯虚数、零可得具体m值.
解答 解:由m2-2m-3=0,得m=-1或m=3;
由m2-3m-4=0,解得m=-1或m=4.
(1)若复数(m2-2m-3)+(m2-3m-4)i为实数,则m2-3m-4=0,即m=-1或m=4;
(2)若复数(m2-2m-3)+(m2-3m-4)i为纯虚数,则m2-2m-3=0且m2-3m-4≠0,即m=3;
(3)若复数(m2-2m-3)+(m2-3m-4)i,则m2-2m-3=0且m2-3m-4=0,即m=-1.
点评 本题考查复数的基本概念,是基础的计算题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
17.如图,在平行四边形ABCD中,E为BC的中点,且$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则( )
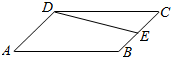

| A. | x=-1,y=-$\frac{1}{2}$ | B. | x=1,y=$\frac{1}{2}$ | C. | x=-1,y=$\frac{1}{2}$ | D. | x=1,y=-$\frac{1}{2}$ |
18.若m>n,则( )
| A. | 0.2m<0.2n | B. | log0.3m>log0.3n | C. | 2m<2n | D. | m2>n2 |
2.若$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(4,k),$\overrightarrow{c}$=$\overrightarrow{0}$,则($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=( )
| A. | 0 | B. | $\overrightarrow{0}$ | C. | 4+2k | D. | 8+k |
12.已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
| A. | 若m∥α,m∥n,则n∥α | B. | 若m⊥α,m∥n,则n⊥α | C. | 若m∥α,n?α,则m∥n | D. | 若m⊥n,n?α,则m⊥α |
19.已知数列$\frac{1}{1×2},\frac{1}{2×3},\frac{1}{3×4},…,\frac{1}{{n×({n+1})}},…$,下面各数中是此数列中的项的是( )
| A. | $\frac{1}{35}$ | B. | $\frac{1}{42}$ | C. | $\frac{1}{48}$ | D. | $\frac{1}{54}$ |
17.若f(x)=cos$\frac{π}{6}$,则f′(x)等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |