题目内容
5.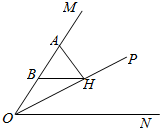 如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
分析 先求出△AHO是直角三角形,再求出∠BHO=∠BOH,∠BOH=∠NOP,由此能证明BH∥ON.
解答  证明:∵AH⊥OP,∴△AHO是直角三角形,
证明:∵AH⊥OP,∴△AHO是直角三角形,
∵B是AO的中点,∴BH=OB(直角三角形斜边中线等于斜边的一半),∴∠BHO=∠BOH(等边对等角),
∵OP平分∠MON,∴∠BOH=∠NOP,
∴∠BHO=∠NOP(等量代换),
∴BH∥ON(内错角相等,两直线平行).
点评 本题考查两直线平行的证明,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
10.两条异面直线是指( )
| A. | 空间中两条不相交的直线 | |
| B. | 不同在任何一个平面内的两条直线 | |
| C. | 分别在两个平面内的两条直线 | |
| D. | 平面内的一条直线和平面外的一条直线 |
17.若f(x)=cos$\frac{π}{6}$,则f′(x)等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
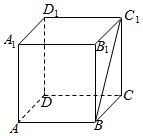 如图所示,在正方体ABCD-A1B1C1D1中,
如图所示,在正方体ABCD-A1B1C1D1中,