题目内容
已知f(x)=3x,并且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].
(1)求函数g(x)的解析式;
(2)求函数g(x)的值域.
(1)求函数g(x)的解析式;
(2)求函数g(x)的值域.
考点:函数的值域,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)利用指数函数的性质求出a的值,然后求g(x)的解析式.
(2)根据指数函数的性质,利用换元法转化为一元二次函数求值域.
(2)根据指数函数的性质,利用换元法转化为一元二次函数求值域.
解答:
解:(1)∵f(a+2)=18,∴3a+2=9•3a=18,即3a=2,∴a=log32,
∴g(x)=3ax-4x=(3a)x-4x=(3log32)x-4x=2x-4x.
(2)∵g(x)=2x-4x=-(2x-
)2+
,
∵-1≤x≤1,
∴
≤2x≤2,
∴设t=2x,则
≤t≤2,
则函数g(x)等价为m(t)=-(t-
)2+
,
∴m(t)单调递减,
∴-2≤m(t)≤
,
即函数g(x)的值域为[-2,
].
∴g(x)=3ax-4x=(3a)x-4x=(3log32)x-4x=2x-4x.
(2)∵g(x)=2x-4x=-(2x-
| 1 |
| 2 |
| 1 |
| 4 |
∵-1≤x≤1,
∴
| 1 |
| 2 |
∴设t=2x,则
| 1 |
| 2 |
则函数g(x)等价为m(t)=-(t-
| 1 |
| 2 |
| 1 |
| 4 |
∴m(t)单调递减,
∴-2≤m(t)≤
| 1 |
| 4 |
即函数g(x)的值域为[-2,
| 1 |
| 4 |
点评:本题主要考查指数函数和二次函数的性质,利用换元法将函数转化为关于t的一元二次函数是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图是一几何体的三视图,则此几何体的体积是( )
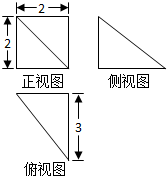

| A、4 | B、8 | C、12 | D、4π |
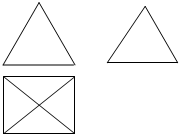 如图是一个空间几何体的三视图,如果主视图和左视图都是边长为2的正三角形,俯视图为正方形,那么该几何体的体积为
如图是一个空间几何体的三视图,如果主视图和左视图都是边长为2的正三角形,俯视图为正方形,那么该几何体的体积为