题目内容
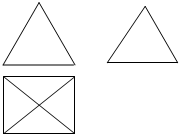如图是一个空间几何体的三视图，如果主视图和左视图都是边长为2的正三角形，俯视图为正方形，那么该几何体的体积为考点：由三视图求面积、体积
专题：计算题
分析：由三视图可知该几何体为四棱锥，根据条件确定四棱锥的底面正方形的边长和棱锥的高，利用锥体的体积公式计算体积即可．
解答：
解：由三视图可知该几何体为四棱锥，底面四边形ABCD边长为2的正方形，
则四棱锥的高VO=
=
，
∴四棱锥的体积为
×2×2×
=
．
故答案为：
．
解：由三视图可知该几何体为四棱锥，底面四边形ABCD边长为2的正方形，则四棱锥的高VO=
| 22-12 |
| 3 |
∴四棱锥的体积为
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
故答案为：
4
| ||
| 3 |
点评：本题主要考查三视图的应用，以及空间几何体的体积计算，要求熟练掌握常见几何体的体积公式．
练习册系列答案
相关题目
若a=log
2，b=20.1，c=(
)0.3，则下列结论成立的是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜c＜a |
| D、b＜a＜c |
设x0是函数f（x）=lnx+x-4的零点，则x0所在的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
已知一个几何体的三视图如图所示，则该几何体的表面积为（ ）| A、24+6π |
| B、24+4π |
| C、28+6π |
| D、28+4π |