题目内容
如图是一几何体的三视图，则此几何体的体积是（ ）
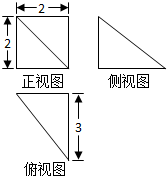
| A、4 | B、8 | C、12 | D、4π |
考点：由三视图求面积、体积
专题：计算题
分析：由三视图可知该几何体的直观图，利用直观图的体积公式进行求解．
解答：
解：
由三视图可知该几何体的为平放的四棱锥，底面为正方形ABCD，边长为2，
侧棱VC⊥面ABCD，且VC=3，
∴三棱锥的体积为
×2×2×3=4，
故选：A．
由三视图可知该几何体的为平放的四棱锥，底面为正方形ABCD，边长为2，侧棱VC⊥面ABCD，且VC=3，
∴三棱锥的体积为
| 1 |
| 3 |
故选：A．
点评：本题主要考查三视图的应用，利用三视图将几何体进行还原是解决三视图题目的关键，要求熟练掌握锥体的体积公式．
练习册系列答案
口算题天天练系列答案
相关题目
已知关于x的方程cos2x+（4t+2）sinx=2t2+2t+1 x∈[0，
]，恰好有三个不等实根，则实数t的取值范围是（ ）
| 3π |
| 2 |
| A、-1≤t≤0 |
| B、-1＜t≤0 |
| C、0≤t≤1 |
| D、0＜t≤1 |
直线l与直线l1：x-3y+10=0和直线l2：2x+y-8=0分别交于M，N两点，且MN的中点坐标为（0，1），则直线l的方程为（ ）
| A、x+4y-4=0 |
| B、4x+y-4=0 |
| C、x-4y+4=0 |
| D、x-4y-4=0 |
若a=log
2，b=20.1，c=(
)0.3，则下列结论成立的是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜c＜a |
| D、b＜a＜c |