题目内容

10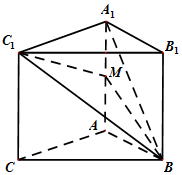．如图，在直三棱柱ABC-A1B1C1中，若四边形AA1C1C是边长为4的正方形，且AB=3，BC=5，M是AA1的中点，则三棱锥A1-MBC1的体积为4．

分析 推导出A1C1⊥平面A1MB，从而三棱锥A1-MBC1的体积${V}_{{A}_{1}-MB{C}_{1}}$=${V}_{{C}_{1}-{A}_{1}MB}$，由此能求出结果．

解答 解：∵在直三棱柱ABC-A1B1C1中，若四边形AA1C1C是边长为4的正方形，且AB=3，BC=5，
∴A1C1⊥AA1，AC2+AB2=BC2，∴A1C1⊥A1B1，
∵AA1∩A1B1=A1，∴A1C1⊥平面A1MB，
∵M是AA1的中点，∴${S}_{△{A}_{1}MB}$=$\frac{1}{2}{S}_{△A{A}_{1}B}$=$\frac{1}{2}×（\frac{1}{2}×3×4）$=3，
∴三棱锥A1-MBC1的体积：
${V}_{{A}_{1}-MB{C}_{1}}$=${V}_{{C}_{1}-{A}_{1}MB}$=$\frac{1}{3}×{S}_{△{A}_{1}MB}×{A}_{1}{C}_{1}$=$\frac{1}{3}×3×4$=4．
故答案为：4．

点评 本题考查几何体的体积的求法，考查空间中线线、线面、面面的位置关系等基础知识，考查推理论证能力、运算求解能力、空间思维能力，考查数形结合思想、化归与转化思想，是中档题．

练习册系列答案
相关题目
20．2016年11月，第十一届中国（珠海）国际航空航天博览会开幕式当天，歼-20的首次亮相给观众留下了极深的印象．某参赛国展示了最新研制的两种型号的无人机，先从参观人员中随机抽取100人对这两种型号的无人机进行评价，评价分为三个等级：优秀、良好、合格．由统计信息可知，甲型号无人机被评为优秀的频率为$\frac{3}{5}$、良好的频率为$\frac{2}{5}$；乙型号无人机被评为优秀的频率为$\frac{7}{10}$，且被评为良好的频率是合格的频率的5倍．
（1）求这100人中对乙型号无人机评为优秀和良好的人数；
（2）如果从这100人中按对甲型号无人机的评价等级用分层抽样的方法抽取5人，然后从其他对乙型号无人机评优秀、良好的人员中各选取1人进行座谈会，会后从这7人中随机抽取2人进行现场操作体验活动，求进行现场操作体验活动的2人都评优秀的概率．
1．已知函数f（x）=cosx（$\sqrt{3}$sinx-cosx）+m（m∈R），将y=f（x）的图象向左平移$\frac{π}{6}$个单位后得到g（x）的图象，且y=g（x）在区间[$\frac{π}{4}$，$\frac{π}{3}$]内的最小值为$\frac{\sqrt{3}}{2}$．
（1）求m的值；
（2）在锐角△ABC中，若g（$\frac{C}{2}$）=-$\frac{1}{2}$+$\sqrt{3}$，求sinA+cosB的取值范围．
18．已知函数$f（x）=\frac{a}{x-2}+lnx$，其中a∈R．
（Ⅰ）给出a的一个取值，使得曲线y=f（x）存在斜率为0的切线，并说明理由；
（Ⅱ）若f（x）存在极小值和极大值，证明：f（x）的极小值大于极大值．
5．已知集合A={-1，0，1，2}，B={1，2，3}，则集合A∪B中所有元素之和是5．
15．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，抛物线E：x2=4y的焦点B是双曲线虚轴上的一个顶点，若线段BF与双曲线C的右支交于点A，且$\overrightarrow{BA}$=3$\overrightarrow{AF}$，则双曲线C的离心率为$\frac{\sqrt{17}}{3}$．
2．将A，B，C，D，E这5名同学从左至右排成一排，则A与B相邻且A与C之间恰好有一名同学的排法有（　　）
A．18B．20C．21D．22
19．已知集合A={x|1＜2x≤16}，B={x|x＜a}，若A∩B=A，则实数a的取值范围是（　　）
A．a＞4B．a≥4C．a≥0D．a＞0
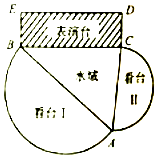20．在水域上建一个演艺广场，演艺广场由看台Ⅰ，看台Ⅱ，三角形水域ABC，及矩形表演台BCDE四个部分构成（如图），看台Ⅰ，看台Ⅱ是分别以AB，AC为直径的两个半圆形区域，且看台Ⅰ的面积是看台Ⅱ的面积的3倍，矩形表演台BCDE 中，CD=10米，三角形水域ABC的面积为$400\sqrt{3}$平方米，设∠BAC=θ．
（1）求BC的长（用含θ的式子表示）；
（2）若表演台每平方米的造价为0.3万元，求表演台的最低造价．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网