题目内容
在△ABC中,角A,B,C所对的边长分别为a,b,c,且cos
=
.
(1)若a=3,b=
,求c的值;
(2)若f(A)=sinA(
cosA-sinA),求f(A)的取值范围.
| A+C |
| 2 |
| 1 |
| 2 |
(1)若a=3,b=
| 7 |
(2)若f(A)=sinA(
| 3 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)已知等式左边变形后,利用诱导公式化简求出sin
的值,确定出B的度数,再由a,b的值,利用余弦定理求出c的值即可;
(2)f(A)解析式去括号后,利用二倍角的正弦、余弦函数公式化简,整理后化为一个角的正弦函数,根据B的度数表示出A+C的度数,确定出这个角的范围,利用正弦函数的值域即可确定出f(A)的范围.
| B |
| 2 |
(2)f(A)解析式去括号后,利用二倍角的正弦、余弦函数公式化简,整理后化为一个角的正弦函数,根据B的度数表示出A+C的度数,确定出这个角的范围,利用正弦函数的值域即可确定出f(A)的范围.
解答:
解:(1)在△ABC中,A+B+C=π,
∴cos
=cos
=sin
=
,
∴
=
,即B=
,
∵a=3,b=
,cosB=
,
∴由余弦定理b2=a2+c2-2accosB,即7=9+c2-3c,
整理得:c2-3c+2=0,
解得:c=1或c=2;
(2)f(A)=sinA(
cosA-sinA)=
sin2A-
=sin(2A+
)-
,
由(1)得B=
,
∴A+C=
,即A∈(0,
),
∴2A+
∈(
,
),
∴sin(2A+
)∈(-1,1],
∴f(A)∈(-
,
],
∴f(A)的取值范围是(-
,
].
∴cos
| A+C |
| 2 |
| π-B |
| 2 |
| B |
| 2 |
| 1 |
| 2 |
∴
| B |
| 2 |
| π |
| 6 |
| π |
| 3 |
∵a=3,b=
| 7 |
| 1 |
| 2 |
∴由余弦定理b2=a2+c2-2accosB,即7=9+c2-3c,
整理得:c2-3c+2=0,
解得:c=1或c=2;
(2)f(A)=sinA(
| 3 |
| ||
| 2 |
| 1-cos2A |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
由(1)得B=
| π |
| 3 |
∴A+C=
| 2π |
| 3 |
| 2π |
| 3 |
∴2A+
| π |
| 6 |
| π |
| 6 |
| 3π |
| 2 |
∴sin(2A+
| π |
| 6 |
∴f(A)∈(-
| 3 |
| 2 |
| 1 |
| 2 |
∴f(A)的取值范围是(-
| 3 |
| 2 |
| 1 |
| 2 |
点评:此题考查了余弦定理,两角和与差的余弦函数公式,余弦函数的定义域与值域,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知下列4个结论中其中正确的序号是 ( )
A、已知cosα=
| |||||||||||
| B、已知2a=3b=k(k≠1)且2a+b=ab,则实数k的值为36 | |||||||||||
C、已知函数f(x)=
| |||||||||||
| D、已知函数f(x)对任意x,y都有f(x+y)=f(x)+f(y)-1,且当x>0时,f(x)>1,若关于x的不等式f(x2-ax+b)<1的解集为{x|-3<x<2},则a+b=-7 |
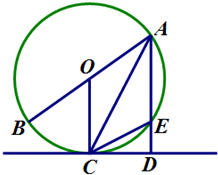 如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,连接AC,过点A作AD⊥CD于点D,交⊙O于点E.
如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,连接AC,过点A作AD⊥CD于点D,交⊙O于点E. 已知函数f(x)=x2-2ax+3在区间[-1,1]上有最小值,记作g(a).
已知函数f(x)=x2-2ax+3在区间[-1,1]上有最小值,记作g(a).