Question

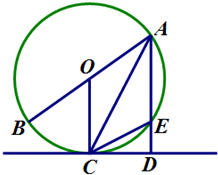如图，已知AB是⊙O的直径，CD是⊙O的切线，C为切点，连接AC，过点A作AD⊥CD于点D，交⊙O于点E．
（Ⅰ）证明：∠AOC=2∠ACD；
（Ⅱ）证明：AB•CD=AC•CE．

Answer 1

考点：与圆有关的比例线段,弦切角

专题：直线与圆

分析：（Ⅰ）连结BC，由已知条件推导出∠ACD=∠ABC，∠OCB=∠ABC，由此能够证明∠AOC=2∠ACD．
（Ⅱ）由已知条件推导出OAC=∠OCA=∠CAE=∠ECD，从而得到Rt△ABC∽Rt△CED，由此能够证明AB•CD=AC•CE．

解答： 证明：（Ⅰ）连结BC，∵CD是⊙O的切线，C为切点，
∴∠ACD=∠ABC，
∵OB=OC，∴∠OCB=∠ABC，
又∵∠AOC=∠OCB+∠OBC，
∴∠AOC=2∠ACD．
（Ⅱ）∵AB是⊙O的直径，∴∠ACB=90°，
又∵AD⊥CD于D，∴∠ADC=90°，
∵CD是⊙O的切线，C为切点，OC为半径，
∴∠OAC=∠CAE，且OC⊥CD，
∴OC∥AD，又∵OC=OA，
∴∠OAC=∠OCA=∠CAE=∠ECD，
∴Rt△ABC∽Rt△CED，∴

AB

CE

=

AC

CD

，
∴AB•CD=AC•CE．

点评：本题考查角相等的证明，考查线段乘积相等的证明，是中档题，解题时要认真审题，注意圆的简单性质的灵活运用．