题目内容
以直角坐标系的原点为极点,x轴非负半轴为极轴,在两种坐标系中取相同单位的长度.已知直线l的方程为
ρcosθ-ρsinθ-1=0(ρ>0),曲线C的参数方程为
(α为参数),点M是曲线C上的一动点.
(Ⅰ)求线段OM的中点P的轨迹方程;
(Ⅱ)求曲线C上的点到直线l的距离的最小值.
ρcosθ-ρsinθ-1=0(ρ>0),曲线C的参数方程为
|
(Ⅰ)求线段OM的中点P的轨迹方程;
(Ⅱ)求曲线C上的点到直线l的距离的最小值.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(Ⅰ)设中点P的坐标为(x,y),依据中点公式求得线段OM的中点P的轨迹的参数方程,再把它化为直角坐标方程.
(Ⅱ)求得直线l的普通方程和曲线C的普通方程,可得曲线C表示以(0,2)为圆心,以2为半径的圆,故所求最小值为圆心(0,2)到直线l的距离减去半径,计算求得结果.
(Ⅱ)求得直线l的普通方程和曲线C的普通方程,可得曲线C表示以(0,2)为圆心,以2为半径的圆,故所求最小值为圆心(0,2)到直线l的距离减去半径,计算求得结果.
解答:
解:(Ⅰ)设中点P的坐标为(x,y),依据中点公式有
(α为参数),
这是点P轨迹的参数方程,消参得点P的直角坐标方程为x2+(y-1)2=1.
(Ⅱ)直线l的普通方程为x-y-1=0,曲线C的普通方程为x2+(y-2)2=4
表示以(0,2)为圆心,以2为半径的圆,
故所求最小值为圆心(0,2)到直线l的距离减去半径,
设所求最小距离为d,则d=
-2=
-2.
因此曲线C上的点到直线l的距离的最小值为
-2.
|
这是点P轨迹的参数方程,消参得点P的直角坐标方程为x2+(y-1)2=1.
(Ⅱ)直线l的普通方程为x-y-1=0,曲线C的普通方程为x2+(y-2)2=4
表示以(0,2)为圆心,以2为半径的圆,
故所求最小值为圆心(0,2)到直线l的距离减去半径,
设所求最小距离为d,则d=
| |0-2-1| | ||
|
3
| ||
| 2 |
因此曲线C上的点到直线l的距离的最小值为
3
| ||
| 2 |
点评:本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,点到直线的距离公式、直线和圆的位置关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设变量x,y满足约束条件
,且目标函数z=y+ax的最小值为-7,则a的值为( )
|
| A、-2 | B、-4 | C、-1 | D、1 |
已知椭圆方程为
+
=1(a>b>0),A、B分别是椭圆长轴的两个端点,M、N是椭圆上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,若|k1•k2|=
,则椭圆的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
若函数f(x)=x2+(a-2)x+6在区间[1,+∞)上是增函数,那么实数a的取值范围是( )
| A、a≥0 | B、a≤0 |
| C、a≥4 | D、a≤4 |
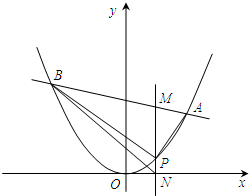 已知抛物线C:x2=2py过点
已知抛物线C:x2=2py过点 已知椭圆C:
已知椭圆C: