题目内容
设m<0,角α的终边经过点P(4m,-3m),那么2sinα+cosα的值等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:利用三角函数的定义即可求得sinα=
=
,cosα=-
,从而可求得答案.
| -3m | ||
|
| 3 |
| 5 |
| 4 |
| 5 |
解答:
解:∵m<0,α的终边经过点P(4m,-3m),
∴sinα=
=
=
,cosα=
=-
,
∴2sinα+cosα=
.
故选:A.
∴sinα=
| -3m | ||
|
| -3m |
| -5m |
| 3 |
| 5 |
| 4m |
| -5m |
| 4 |
| 5 |
∴2sinα+cosα=
| 2 |
| 5 |
故选:A.
点评:本题考查任意角的三角函数的定义,考查运算求解能力,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
某产品生产厂家的市场部在对4家商场进行调研时,获得该产品售价x(单位:元)和销售量y(单位:件)之间的四组数据如表:
为决策产品的市场指导价,用最小二乘法求得销售量y与售价x之间的线性回归方程y=-1.4x+a,那么方程中的a值为( )
| 售价x | 4 | 4.5 | 5.5 | 6 |
| 销售量y | 12 | 11 | 10 | 9 |
| A、17 | B、17.5 |
| C、18 | D、18.5 |
半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是( )
| A、πR2 |
| B、2πR2 |
| C、3πR2 |
| D、4πR2 |
设复数z1=1+i,z2=2+xi(x∈R),若z1•z2∈R,则x=( )
| A、-2? | B、-1? | C、1 | D、2 |
如图是一个几何体的三视图,由图中数据可知该几何体中最长棱的长度是( )


| A、6 | ||
B、2
| ||
| C、5 | ||
D、
|
 一个几何体的三视图如图所示,主视图与侧视图都是边长为
一个几何体的三视图如图所示,主视图与侧视图都是边长为2的正三角形,俯视图为正方形,则该几何体的全面积为( )
| A、4 | ||
| B、8 | ||
| C、12 | ||
D、4+4
|
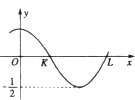 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(| 1 |
| 6 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、
|
 高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示,如图所示.
高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示,如图所示.