Question

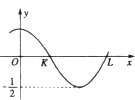设偶函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，KL=1，则f（

1

6

）的值为（　　）

• A、-

  3

  4

• B、-

  1

  4

• C、-

  1

  2

• D、

  3

  4

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由图可知，A=

1

2

，T=

2π

ω

=2，从而可求得ω=π，再由f（0）=

1

2

sinφ=

1

2

，0＜φ＜π，可求得φ=

π

2

，于是可得函数f（x）=Asin（ωx+φ）的解析式，从而可求f（

1

6

）的值．

解答： 解：∵KL=

1

2

T=1，ω＞0，
∴T=

2π

ω

=2，
∴ω=π，又A=

1

2

，
∴f（x）=

1

2

sin（πx+φ），
又f（0）=

1

2

sinφ=

1

2

，0＜φ＜π，
∴φ=

π

2

，
∴f（x）=

1

2

sin（πx+

π

2

）=

1

2

cosπx，
∴f（

1

6

）=

1

2

cos

π

6

=

3

4

．
故选：D．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求得ω=π，φ=

π

2

，是关键，也是难点，考查识图与运算求解能力，属于中档题．