题目内容
计算:1•2+2•22+3•22+…+(n-1)•2n-1.
考点:数列的求和
专题:等差数列与等比数列
分析:利用“错位相减法”、等比数列的前n项和公式即可得出.
解答:
解:设Sn=1•2+2•22+3•22+…+(n-1)•2n-1.
则2Sn=1×22+2×23+…+(n-2)×2n-1+(n-1)×2n,
∴-Sn=2+22+23+…+2n-1-(n-1)×2n=
-(n-1)×2n=(2-n)×2n-2,
∴Sn=(n-2)×2n+2.
则2Sn=1×22+2×23+…+(n-2)×2n-1+(n-1)×2n,
∴-Sn=2+22+23+…+2n-1-(n-1)×2n=
| 2(2n-1-1) |
| 2-1 |
∴Sn=(n-2)×2n+2.
点评:本题考查了“错位相减法”、等比数列的前n项和公式,属于基础题.

练习册系列答案
相关题目
已知函数f(x),下列函数图象关于直线x=3对称的有( )
①y=f(x+3)②y=f(x-3)③y=f(3-x) ④y=-f(x+3)⑤y=-f(x-3)⑥y=-f(3-x).
①y=f(x+3)②y=f(x-3)③y=f(3-x) ④y=-f(x+3)⑤y=-f(x-3)⑥y=-f(3-x).
| A、②和③,⑤和⑥ |
| B、①和③ |
| C、③和⑤ |
| D、④和⑤,②和③ |
设数列{an}的前n项和为Sn,且满足an+Sn=1,则Sn的取值范围是( )
| A、(0,1) | ||
| B、(0,+∞) | ||
C、[
| ||
D、[
|
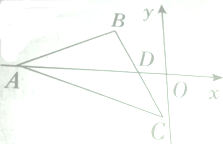 在平面直角坐标系xOy中,A(-4,0)D(-1,0),设△ABC是等腰三角形,点B在x轴上方,且BA=BC,D为BC的中点 若△ABC是正三角形,求直线AB的方程.
在平面直角坐标系xOy中,A(-4,0)D(-1,0),设△ABC是等腰三角形,点B在x轴上方,且BA=BC,D为BC的中点 若△ABC是正三角形,求直线AB的方程.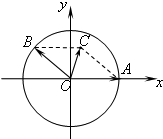 如图所示,在xOy平面上,点A(1,0),点B在单位圆上.∠AOB=θ(0<θ<π)
如图所示,在xOy平面上,点A(1,0),点B在单位圆上.∠AOB=θ(0<θ<π)