题目内容
在平面直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线C:ρsin2θ=2acosθ(a>0),过点P(-2,-4)的直线l的参数方程为
(t为参数).直线l与曲线C分别交于M、N.若|PM|、|MN|、|PN|成等比数列,求实数a的值.
|
考点:参数方程化成普通方程
专题:
分析:由曲线C:ρsin2θ=2acosθ(a>0),化为ρ2sin2θ=2aρcosθ,可得直角坐标方程,将直线l的参数方程化为标准形式
(t′为参数),代入曲线C的直角坐标方程得:
t′2-(4
+
a)t′+16+4a=0,由于直线与曲线交于两点,可得△>0.设交点M,N对应的参数分别为t1′,t2′.可得根与系数的关系,若|PM|、|MN|、|PN|成等比数列,可得|t1′-t2′|2=|t1′t2′|,解出即可.
|
| 1 |
| 2 |
| 2 |
| 2 |
解答:
解:由曲线C:ρsin2θ=2acosθ(a>0),化为ρ2sin2θ=2aρcosθ,可得直角坐标方程为y2=2ax (a>0),
将直线l的参数方程化为标准形式
(t′为参数),
代入曲线C的直角坐标方程得:
t′2-(4
+
a)t′+16+4a=0,
∵直线与曲线交于两点,
∴△>0,即a>0或a<-4.
设交点M,N对应的参数分别为t1′,t2′.
则t1′+t2′=2(4
+
a),t1′t2′=2(16+4a).
若|PM|、|MN|、|PN|成等比数列,
则|t1′-t2′|2=|t1′t2′|,
解得a=1或a=-4(舍)
所以满足条件的a=1.
将直线l的参数方程化为标准形式
|
代入曲线C的直角坐标方程得:
| 1 |
| 2 |
| 2 |
| 2 |
∵直线与曲线交于两点,
∴△>0,即a>0或a<-4.
设交点M,N对应的参数分别为t1′,t2′.
则t1′+t2′=2(4
| 2 |
| 2 |
若|PM|、|MN|、|PN|成等比数列,
则|t1′-t2′|2=|t1′t2′|,
解得a=1或a=-4(舍)
所以满足条件的a=1.
点评:本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、参数的应用、等比数列的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x),下列函数图象关于直线x=3对称的有( )
①y=f(x+3)②y=f(x-3)③y=f(3-x) ④y=-f(x+3)⑤y=-f(x-3)⑥y=-f(3-x).
①y=f(x+3)②y=f(x-3)③y=f(3-x) ④y=-f(x+3)⑤y=-f(x-3)⑥y=-f(3-x).
| A、②和③,⑤和⑥ |
| B、①和③ |
| C、③和⑤ |
| D、④和⑤,②和③ |
设数列{an}的前n项和为Sn,且满足an+Sn=1,则Sn的取值范围是( )
| A、(0,1) | ||
| B、(0,+∞) | ||
C、[
| ||
D、[
|
当n=4时,执行如图所示的程序框图,输出的S值为( )


| A、6 | B、8 | C、14 | D、30 |
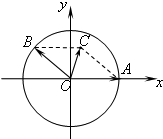 如图所示,在xOy平面上,点A(1,0),点B在单位圆上.∠AOB=θ(0<θ<π)
如图所示,在xOy平面上,点A(1,0),点B在单位圆上.∠AOB=θ(0<θ<π)