题目内容
已知函数g(x)=(
)x与函数y=f(x)的图象关于直线y=x对称,若a=g(0.2),b=f(2),c=f(0.2),则( )
| 1 |
| 3 |
| A、a<b<c |
| B、b<a<c |
| C、a<c<b |
| D、c<b<a |
考点:反函数
专题:函数的性质及应用
分析:根据函数g(x)=(
)x与函数y=f(x)的图象关于直线y=x对称,求出f(x);求出a,b,c判定出a,b,c的范围即得到答案.
| 1 |
| 3 |
解答:
解:∵函数g(x)=(
)x与函数y=f(x)的图象关于直线y=x对称,
∴f(x)=log
x
∴a=g(0.2)=(
)0.2,b=f(2)=log
2,c=f(0.2)=log
0.2,
∵0<(
)0.2<1,log
2<0,=log
0.2>1
∴b<a<c
故选B
| 1 |
| 3 |
∴f(x)=log
| 1 |
| 3 |
∴a=g(0.2)=(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∵0<(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴b<a<c
故选B
点评:本题考查反函数,用好反函数的性质是解决问题的关键,属基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
下列函数为周期函数的是( )
| A、f(x)=sinx,x∈[0,2π] | ||
B、f(x)=
| ||
| C、f(x)=sin|x| | ||
| D、f(x)=2014(x∈Z) |
函数y=
+
是( )
| 1-|x| |
| 9 |
| 1+x2 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
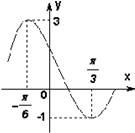 已知三角函数f(x)=Acos(ωx+φ)+b(A>ω>0,|φ|<
已知三角函数f(x)=Acos(ωx+φ)+b(A>ω>0,|φ|< 已知函数f(x)为奇函数,当x≥0时,f(x)=
已知函数f(x)为奇函数,当x≥0时,f(x)=