题目内容
11.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=2x3-3x2+$\frac{3}{2}$,则g($\frac{1}{100}$)+g($\frac{2}{100}$)+…+g($\frac{99}{100}$)=( )| A. | 100 | B. | 99 | C. | 50 | D. | 0 |
分析 由题意对已知函数求两次导数可得图象关于点($\frac{1}{2}$,1)对称,即f(x)+f(1-x)=2,即可得到结论.
解答 解:∵g(x)=2x3-3x2+$\frac{3}{2}$,
∴g′(x)=6x2-6x,g″(x)=12x-6,
令g″(x)=0,解得:x=$\frac{1}{2}$,
而g($\frac{1}{2}$)=1,
故函数g(x)关于点($\frac{1}{2}$,1)对称,
∴g(x)+g(1-x)=2,
∴g($\frac{1}{100}$)+g($\frac{2}{100}$)+…+g($\frac{99}{100}$)
=g($\frac{1}{100}$)+g($\frac{99}{100}$)+g($\frac{2}{100}$)+g($\frac{98}{100}$)+…+g($\frac{49}{100}$)+g($\frac{51}{100}$)+g($\frac{1}{2}$)
=2×49+1=99,
故选:B.
点评 本题主要考查导数的基本运算,利用条件求出函数的对称中心是解决本题的关键.求和的过程中使用了倒序相加法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知集合A={1,3,$\sqrt{m}$},B={1,m},A∩B={1,m},则m=( )
| A. | 0或$\sqrt{3}$ | B. | 0或3 | C. | 1或3 | D. | 1或3或0 |
2.在等比数列{an}中,若a6=6,a9=9,则a3为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{16}{9}$ | D. | 4 |
6.下列四个命题中真命题为( )
| A. | lg(x2+1)≥0 | B. | 5≤2 | C. | 若x2=4,则x=2 | D. | 若x<2,则$\frac{1}{x}$>$\frac{1}{2}$ |
3.去A城市旅游有三条不同路线,甲、乙两位同学各自选择其中一条线路去A城市旅游,若每位同学选择每一条线路的可能性相同,则这两位同学选择同一条路线的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{9}$ |
20.已知数列{an}:a1=1,${a_{n+1}}=2{a_n}+3,({n∈{N^+}})$,则an=( )
| A. | 2n+1-3 | B. | 2n-1 | C. | 2n+1 | D. | 2n+2-7 |
1.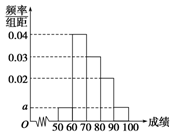 某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
(Ⅰ)求图中a的值;
(Ⅱ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.
 某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].(Ⅰ)求图中a的值;
(Ⅱ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |