题目内容
1.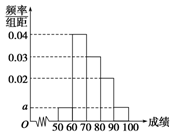 某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].(Ⅰ)求图中a的值;
(Ⅱ)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
分析 (Ⅰ)根据频率和为1列出方程即可求出a的值;
(Ⅱ)利用表中数据计算数学成绩在[50,90)内的人数,再求在[50,90)之外的人数.
解答 解:(Ⅰ)根据频率分布直方图中各个小矩形的面积和等于1得,
10×(2a+0.02+0.03+0.04)=1,
解得a=0.005,
所以图中a的值为0.005;
(Ⅱ)数学成绩在[50,60)的人数为:100×0.05×1=5(人);
数学成绩在[60,70)的人数为:100×0.4×$\frac{1}{2}$=20(人);
数学成绩在[70,80)的人数为:100×0.3×$\frac{4}{3}$=40(人);
数学成绩在[80,90)的人数为:100×0.2×$\frac{5}{4}$=25(人);
所以数学成绩在[50,90)之外的人数为:100-5-20-40-25=10(人).
点评 本题考查频率分布直方图的应用问题,也考查了识图、用图的能力,是基础题目.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
12.如图是一个几何体的三视图,则该几何体的体积为( )


| A. | 9π | B. | 18π | C. | 27π | D. | 54π |
9.在空间直角坐标系中,点(-2,1,5)关于x轴的对称点的坐标为( )
| A. | (-2,1,-5) | B. | (-2,-1,-5) | C. | (2,-1,5) | D. | (2,1,-5) |
16.在区间[0,1]上任取两个实数a,b,则函数f(x)=x2+ax+b2无零点的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
6. 如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( )
如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( )
 如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( )
如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( )| A. | 平行 | B. | 相交成60° | C. | 相交且垂直 | D. | 异面直线 |
10.已知集合A={x|(x-1)(x-3)<0},B={x|2<x<4},则A∩B=( )
| A. | {x|1<x<3} | B. | {x|1<x<4} | C. | {x|2<x<3} | D. | {x|2<x<4} |
11.已知实数a,b,c满足a2+2b2+3c2=1,则a+2b的最大值是( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
 某四面体的三视图如图所示,则此四面体的四个面中面积最大的面的面积等于$2\sqrt{3}$.
某四面体的三视图如图所示,则此四面体的四个面中面积最大的面的面积等于$2\sqrt{3}$.