题目内容
19.函数y=$\frac{{x}^{2}+2x+1}{{x}^{2}+4x}$(x>0)的最小值是$\frac{3}{4}$.分析 令x+1=t(t>1),则y=$\frac{{t}^{2}}{{t}^{2}+2t-3}$=$\frac{1}{1+\frac{2}{t}-\frac{3}{{t}^{2}}}$,运用配方法,即可得到所求最小值.
解答 解:y=$\frac{(x+1)^{2}}{{x}^{2}+4x}$,
令x+1=t(t>1),
则y=$\frac{{t}^{2}}{{t}^{2}+2t-3}$=$\frac{1}{1+\frac{2}{t}-\frac{3}{{t}^{2}}}$
=$\frac{1}{-3(\frac{1}{t}-\frac{1}{3})+\frac{4}{3}}$,
当$\frac{1}{t}$=$\frac{1}{3}$,即t=3,即x=2时,取得最小值$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查函数的最值的求法,注意运用换元法和配方法,考查运算能力,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
7.已知F1、F2分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的左右两个焦点,过F1作倾斜角为$\frac{π}{4}$的弦AB,则△F2AB的面积为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$-1 |
14.设x,y∈[0,1],则满足y>$\sqrt{1-{x}^{2}}$的概率为( )
| A. | 1-$\frac{π}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
8.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为$2\sqrt{3}$,AB=2,AC=1,∠BAC=60°,则此球的表面积等于( )
| A. | 5π | B. | 20π | C. | 8π | D. | 16π |
9.在空间直角坐标系中,点(-2,1,5)关于x轴的对称点的坐标为( )
| A. | (-2,1,-5) | B. | (-2,-1,-5) | C. | (2,-1,5) | D. | (2,1,-5) |
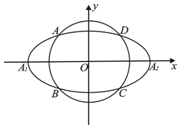 如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.